数学月間(第1日目)の2番目の講演[2024.7.22,15:20-16:50]は,
「世界の数学者ゆかりの地を訪ねて」仙田章雄(埼玉県立浦和第一女子高等学校)でした.仙田章雄氏は,浦和高校,浦和第一女子高校を通して,37年間,数学通信「気まぐれ」の発行を続けておられます.
講演者は,1987~2019年の32年間のほとんど毎夏休みごとに,世界の数学者ゆかりの地の旅をしています.基本的に一人旅です.本日の講演では,(1)ピタゴラス(ギリシャ,イタリア),(2)プラフマグプタ(インド),(3)オイラー他(ヨーロッパ)の旅が紹介されました.用いたスライドは140枚にもなります.
ところで,この講演を聴講した筆者は,講演録を書く段になって,思わぬ困難に直面することになりました.これらの地は,忘れ去られた辺鄙な地,廃墟のような地であったりします.これらのターゲットは,必ずしも,風光明媚な観光地と言うわけではなく,数学に興味を持つ者のみが関心をもつ地であります.
一般の人に,「ピタゴラスの洞窟」と言っても,「何だそれは」となります.「ブラフマグプタのウッジャイン天文台」と言っても,「何だそれは」.「オイラーの散歩とケーニヒスブルクの橋」と言っても「何だそれは」です.
講演を聴く側に数学的背景知識がなければ,これらの価値はわからない.
従って,講演録の筆者は,それらの背景をある程度説明せねばなりませんが最小限に留めました.できるだけ本質的な記述をしようとすると,それらの底にある数学史の大きな流れに言及せざるを得ず,講演録筆者の独断で,最後にイスラム(アラビア)の数学の役割を付け加えました.
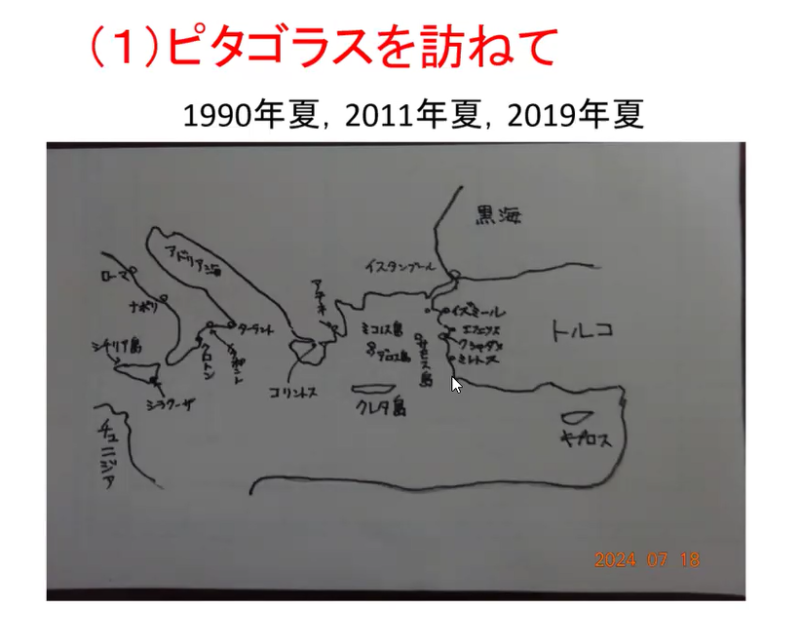
(1)ピタゴラス
1990年(第1回)ギリシャ,2011年(第2回)ギリシャ,2019年(第3回)イタリアの3回の旅行があります.
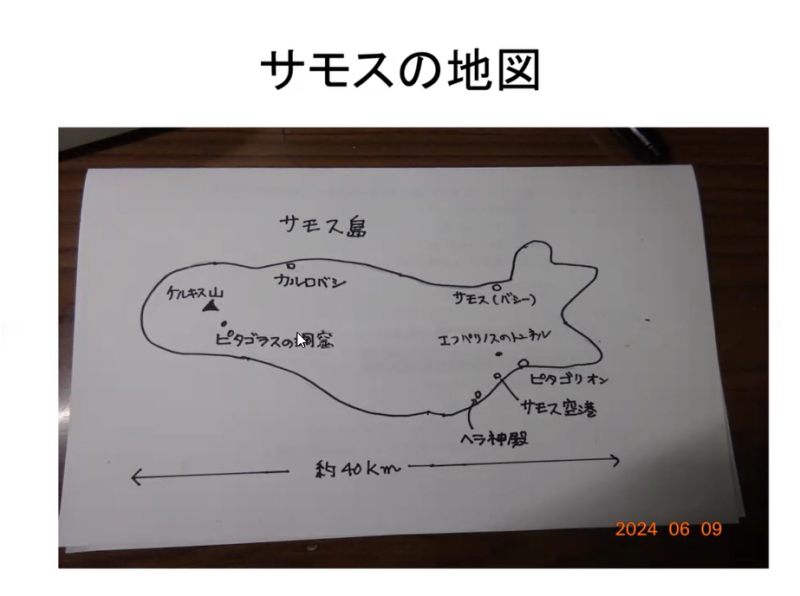
①第1回目は,アテネ→イスタンブール→イズミール→クシャダスから30人乗りほどの小さい船でサモス島に向かいました.
ピタゴラスの洞窟は,サモス島のカルロバシにあります.ピタゴラス(紀元前582年 - 紀元前496年)は国王から迫害されていましたので,学園の弟子たちと洞窟に隠れて生活していたこともあったでしょう.
②第2回目は,アテネ→ミコノスからフェリーでサモス島に向かいました.
デロス島(無人島)にはミコノスから船で日帰りします.
デロス島には倍積問題で有名な「デロスの祭壇」があります.
デロス島にはミコノス島から日帰りします.
ピタゴリオンは,ピタゴラスの他に,アリスタルコス,イソップのゆかりの地でもあります.
③第3回目は,イタリアです.ナポリ→ターラント→クロトン.
ターラント城は海軍の施設(見学もできます).ピタゴラス通り旧市街は廃墟感が溢れています.クロトンには充実したピタゴラス博物館があります.ピタゴラス学園を見るにはタクシーに乗らないと行けません.
(2)ブラフマグプタ
ブラフマグプタ(598~665年)は,円に内接する四辺形の面積で,三角形でのヘロンの公式の一般化を発見しました.また,2次方程式の解の公式を初めて発見しました.
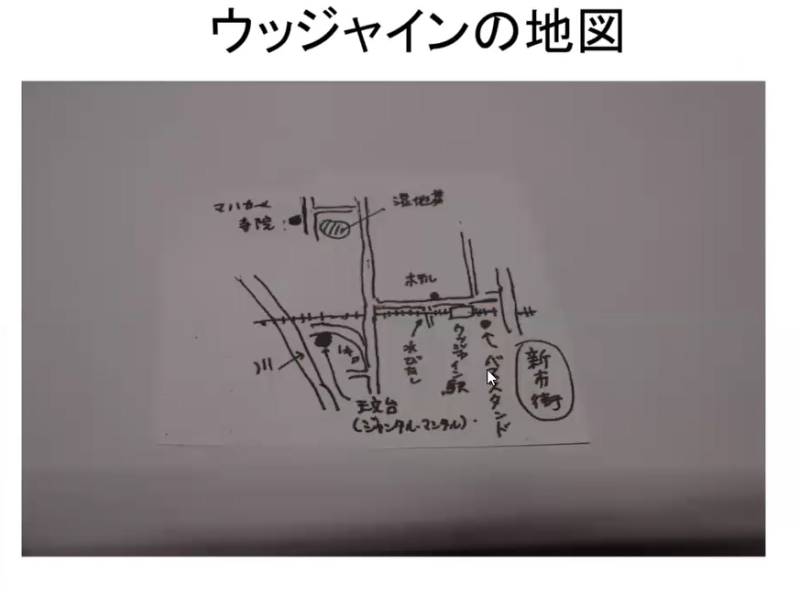
ムンバイ駅から寝台列車でウッジャインに向かいます.ウッジャインには野良牛がたくさんいます.
ブラフマグプタはウッジャインの天文台長を務めました.
(3)リーマン,ガウス,ラマヌジャン,ハミルトン,アーベル,ガロア,オイラー
リーマン
ガウス
ゲッチンゲンにあるガウスの記念碑の台座の後ろにある図形が「正17角形」との記述が色々な文献で見られるが,「正17角形」ではなかった.どの文献にどのように記述されているかを,講演後に仙田氏が調査した.それらは,講演資料に追加し公開してある.
(講演録筆者注)ーーーーー
このような図形は星形正17角形と呼ぶ.星型の頂点で辺の方向は,$${16\pi/17}$$だけ向きを変え,閉じた星型図形ができたときには,辺は16回回転している.我々は,そのような星型を正17/16角形と呼んでいる.正17角形の場合は,頂点で辺は$${2\pi/17}$$だけ方向を変え,17の頂点で回り終わり閉じた図形ができると辺の向きは1回転($${2\pi}$$)する.従って,正17/1=17角形と記述できる.
ーーーーーーーーーーーーー
ラマヌジャン
インドのクンバコナムにある
ハミルトン
アーベル
ガロワ
オイラー
ケーニヒスベルク(ロシアの飛び地で,現在はカリーニングラード)にある7つの橋を全て1度ずつ通って戻ってくるルートが存在するかという一筆書きの問題で知られる.現在は工事され6つの橋になってしまった.
■補足:数学史の流れ(講演録筆者より)
古代エジプトやギリシャに始まった数学や科学は,8世紀には繁栄を極めたイスラム帝国の都バクダッドに集まっていきます.インドの数学も同様です.バクダッドはあらゆる文化の集積地,坩堝であり,数学や科学も大きな発展をしました.その時代のヨーロッパはキリスト教の中世暗黒時代であり,ルネッサンスの夜明けを待つてイスラムからの学芸が流れ込む前夜でありました.アラビアでは,エジプトやインドから伝えられたゼロの概念を取り入れて,アラビア数字や10進法が確立しました.イスラムの数学は,代数学や三角関数などの実際的な発展に特徴があります.講演録の筆者は,これらの遺跡を探す旅を想像します.しかし残念なことに,イラク戦争が起こり,かつて平和の都として栄えたバクダッドで何の痕跡も見いだせないような気がしています.
8世紀に成立したアッバース朝では,カリフや宮廷のワズィールたちが保護をうけ,第7代カリフ,マアムーンが創設した研究施設バイト・アル=ヒクマ(智恵の館)には多くの科学者が集まり,ギリシャ科学のアラビア語への翻訳が進めらました.マアムーンに仕えた科学者・数学者のひとりが,
フワーリズミー(780頃~850頃)でした.
科学では,古代エジプトに起源を持つ錬金術の実験が繰り返され,元素記号が生まれ,文学では,アラビアン=ナイトが生まれ,唐で発明された製紙法もキルギスの戦いの際に伝わりました.
バクダッドには100軒を越す書店があったそうです.
百花繚乱.当時のバグダッドのにぎわいと言ったらすごい.見たかったですね.イブン・シーナは最先端医学の医学典範を著し,世界初の総合病院がバクダッドに作られました.
病院は寄進され,その運営費も,周辺の市場の売り上げ寄付で行うワクフという相互扶助の制度が,公共施設を支えたそうです.
円城都市を中心に,モスク3万,多くの市場と市場には100店を超す店があったそうです.500年間繁栄したイスラム帝国は,1万2千のモンゴル軍により滅亡しました.チグリス川は血で染まり,本のインクで青く染まったそうです.
アラビア語に訳されたアリストテレスなどギリシャの古典や発展したイスラムの科学は,その後ヨーロッパに伝わりラテン語に翻訳されルネッサンスが花開きます.
「イスラムの数学と都市の発展」につては,以下の記事をご覧ください.
https://note.com/sgk2005/n/nbf7f7d38d7f8