<<音楽とは,無意識になされる魂の秘密の代数演算である>>ヨハン・セバスティアン・バッハと同時代に生きた解析学の創始者の一人であるゴットフリート・ライプニッツが,クリスティアン・ゴールトバッハ宛の書簡(1712年4月27日)の中に,この偉大な言葉を書いたのは今から300年前である.今日,数学が提供するのは,既存の音楽作品を研究し,その知識を生徒たちに伝えるためのアプローチだけではない.新たな創造の可能性,音楽を「構築」する新たな方法も提供している.音楽は楽譜を使って保存され伝達される.楽譜には,音程,開始時間,演奏時間,音量,演奏される楽器などの情報が含まれている.連続するシーケンスをどのように変形すれば,オリジナルと同時または連続演奏しても面白く魅力的なメロディーになるだるうか?対位法人間が幼少期に習得する最も単純な数学演算は足し算と引き算である.音楽家が教わるメロディの最も単純な変換は移調である.移調とは,音楽シーケンスの各音符の音程を,固定された一定の音楽単位(半音)だけ変えることである.複数の声部がある場合,ある声部を他の声部に対し相対的に移調することは,「垂直対位法」と呼ばれる.セルゲイ・イヴァノヴィチ・タネーエフの著作『厳密な書法による可動対位法』(1906年)において,一般的な対位法を記述する数式形式が提示された.以下は,この教科書に掲載されている垂直対位法の「モデル」例である.
最初は2つのメロディ・パターン(声部)がある.上の はそのままで,第2声部が1クオート下がる.
*訳者解説)1クォート下がるとは,完全4度下がることである.ハ音記号の楽譜は中心線がC音である.左側の楽譜の第2声の音はCで始まるが,右側の楽譜の第2声の音はGで始まり,完全4度下がっている.第2声の左側の楽譜のメロディは,右側の楽譜では完全4度下がってそのまま再現される.ーーーーーーーーーーーー
そして,次はヨハン・セバスティアン・バッハの作品からの一例で,「平均律クラヴィーア曲集」(1744年)の第1部にあるホ短調 のフーガである.これは2つの19連打の部分と4連打のコーダ(終結部)で構成されている.第2楽章は,第1楽章のほぼ正確な垂直対位法で,両声部がずれている.たとえば,第1楽章(第16-17-18小節)と第2楽章の(第31-32-33小節)の2つの断片を比べてみよう.
第1声部と第2声部の位置が変わっているのは容易にわかる.高声部が下方に,低声部が上方に移動しているのだ.つまり,それぞれの声部に異なる垂直対位法が適用されている.アルベルト・シュヴァイツァーが書いているように,バッハの作品は長い間過小評価されてきた.それは彼の作品の音符が,深い音楽的内容を伴わない,単に形式的に美しいテキストとして認識されていたからである.しかし,歴史は,形式的な構成がとっても驚くほど耳に美しいものであることを証明している.
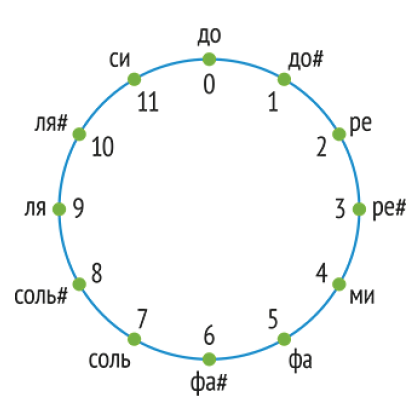
モジュロ$${n}$$($${n}$$を法とする算術)
音階における音符の周期性は,数学における周期集合とよく似ている.これは作曲における形式的な数学手法を生み出した.整数の世界では,等号の概念の特別な拡張がある:2つの整数$${a}$$および$${b}$$は,その差$${a - b}$$が$${n}$$で割り切れる場合,つまり,$${a≡b(mod n)}$$である場合,自然数$${n}$$を法として(モジュロ$${n}$$として)等しいと呼ばれる.これを用いて,偉大な数学者C.F.ガウスは,新しい構造modulo $${n}$$演算(1801年)を提案した.この算術に従い,数は足し算,引き算,掛け算,そして時には 割り算もできる.
例えば,モジュロ$${n}$$が12であれば,この算術にはちょうど12種類の数が存在することになる.これら12種の代表は次のように選ぶ.自然数を12で割った余り$$ \{0, 1, ..., 10, 11 \} $$を代表とするのである. 演算の例:8 +5 ≡ 1, 8 ・ 5 ≡ 4。半音階スケールとの類似性:半音の12音からなる1周期は,1オクターブ.第1オクターブのD音に12半音を加えると,第2オクターブのD音になる.オクターブは調和することが知られている.ーーーこのアプローチは1844年にさかのぼる.その作者であるフランスの音楽学者カミーユ・デュルトは,一様に調律されたピアノでは,多くの音程が12段階の周期に分けられることを指摘した.このことから,音程に対する演算は「モジュロ12」と定義された.このような考え方を作曲に応用することで,アメリカの作曲家ミルトン・バビットは,いわゆる「集合論」(1992年)という音楽理論全体を作り上げ,数学論文に発表した.
和声分析
最も単純な倍音は,三角関数$${1,cos kx,sin kx}$$($${k}$$は任意の自然数)である.これらの関数は,数学と音響学の両方で特別な役割を果たしている.以下の問題は調和解析の基本的な問題である: 与えられた関数を三角級数の和として表現すること,与えられた性質を持つ関数をそのような級数の和として求めること(例えば,ある初期条件と境界条件を満たす微分方程式の解).
*訳者注)Fourier解析のこと.
音楽音響学では,これらの問題の第一は,H.L.F.ヘルムホルツによって提案され,ドーム型共振器(「ヘルムホルツ共振器」)のシステムを用いた音の研究方法で,これによって音のスペクトル組成を決定することが可能になった.第二の問題は,加法合成の出現のきっかけとなったことである.加法合成は,20世紀の音楽における最も輝かしいトレンドの1つである.この様式は,多数の単純な倍音の重ね合わせによって得られる人工的な音で構成されている.現代のコンピューター技術の水準は,機械的な装置を使わないことを可能にしている.特に,フランスの作曲家ジャン=クロード・リッセは、このスタイルで確固たる地位を築いている. 鐘の音を思わせる電子音のセットを手に入れた.これが 彼の作曲した『Mutations』(1969年)の基礎となっている.
確率論
確率論的手法の作曲への応用は,ジャニス・クセナキスによって提唱された.クセナキスはエンジニアとして訓練を受け,ル・コルビュジエのもとで働き,建築家として認められるようになった.一方,彼は生涯音楽に携わり,著名な作曲家となっただけでなく,音楽学者・理論家にもなった.彼の仕事,業績,情熱を統合していたのものは,至るところで数学的手法を応用したり,応用の機会を探したりしていたことだった.例えば,直線の動きを利用するというアイデアは,1954年の音楽作品『メタスタシス』では,弦楽器の連続的なグリッサンドとして,ブリュッセルで開催された万国博覧会「Expo-58」のフィリップス・パビリオンでは,屋根の表面を直線で構成したことに共通している.
選択された数学的モデルに従って楽曲がダイナミックに展開するというアイデアは,その後何年にもわたり彼によって発展させられた.このモデルはランダムな過程によって定義され,ある瞬間に作者が意図した信号スペクトルや空間上の音量分布などが得られるように選択された.クセナキスの音楽的マニフェストは,著書『形式化された音楽』(1963年),ロシア語訳(2008年)である.特にこの本では,集合論,確率論,情報理論,ゲーム理論といった数学の分野を,音楽の作曲や研究に応用することを探求している.
アルゴリズム論
よく知られているように,アルゴリズムとは,有限のステップ数で目標を達成するための実行者の行動順序を記述した命令の集合である.同じアルゴリズムが入力データに順次適用される場合,そのようなプロセスは反復と呼ばれる.数学では,反復プロセスの最も一般的なバリエーションは,逐次近似の方法によって問題の解を見つけることである.また, "探索的 "と呼ばれるあらかじめ決められたゴールのないプロセスのバリエーションがある.日常生活においても,反復プロセスは珍しくない.例えば,現在の銀行預金に年利が発生すると,次年の預金額が増える.(複利と呼ばれる).
応用:音楽
数学: 調和分析、モジュラー算術、確率論、アルゴリズム
『数学構成要素』p.202-205 Амосов Григорий Геннадьевич