式(4)と式(9)が厳密な無限空間上で成立することを考えると,このような準結晶に触発された波動関数が,有限系,例えばトーラスや環の上でも実現できるのか問いたくなる.PTsには根本的な障害がある:図2の矢印は非周期的なマッチングルールを定義している:局所的にペンローズタイリングに似ている,つまりマッチングルールに従うどのようなタイリングも非周期的でなければならず,それゆえトーラス上では決して実現できない.実際,トーラス上のPTに似た配置は,少なくとも2つの「欠陥」を含んでいなければならない[27].
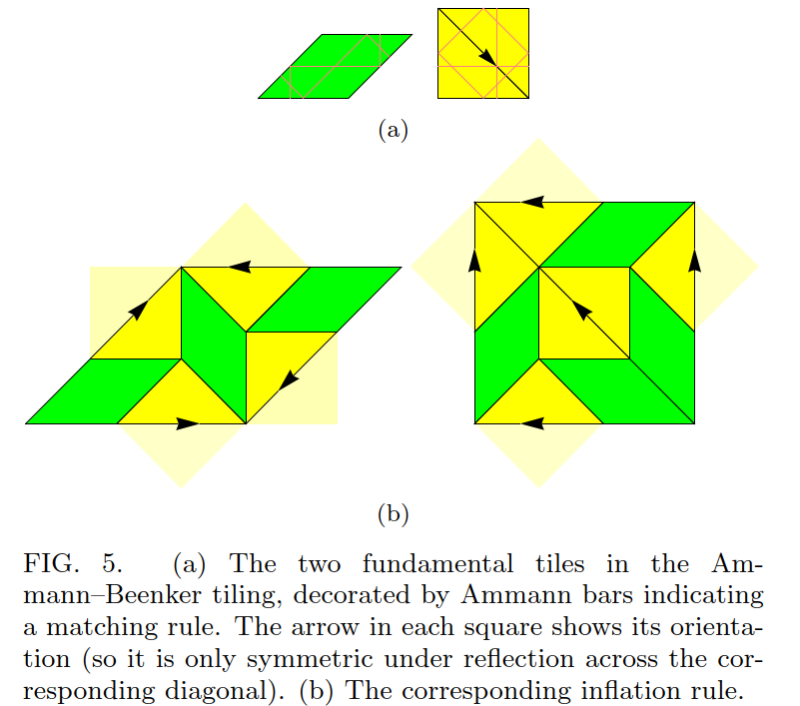
幸運なことに,この障害を回避できるタイリングがいくつかある.その一例が Ammann-Beenker(AB)タイリング [3, 18-20]である.ABタイリングは,図5に示すインフレーションルールで定義される.
ABタイリングはPTと多くの類似した性質を共有している.例えば,非周期で、周期的結晶では禁じられている一種の準回転対称性( ABタイリングの場合は8回,PTタイリングの場合は10回)を持つ.各タイルにはアンマン棒[28, 29]が付いており,これらはまっすぐな切れ目のないアンマン線に結合しなければならない.
しかし,PTとは異なり,ABタイリングには非周期的なマッチング規則 [30]がない.ABタイリングの許容される局所的なパターン(どんなに大きくても)の有限集合が与えられても,$${R^2}$$には周期近似[31, 32]で知られる周期的なタイリングが存在する.このような周期的なABタイリング は正真正銘のABティリングではなく,(それを定義するインフレーション/デフレーション規則によって)非周期的でなければならない.示
とはいえ,これらの周期的なAB様のタイリング(任意に選んだスケールで,局所的には本物のABタイリングと識別できないように構成できる)を利用して,式(4)と同様の方法で量子エラー訂正波動関数を構成することができる.
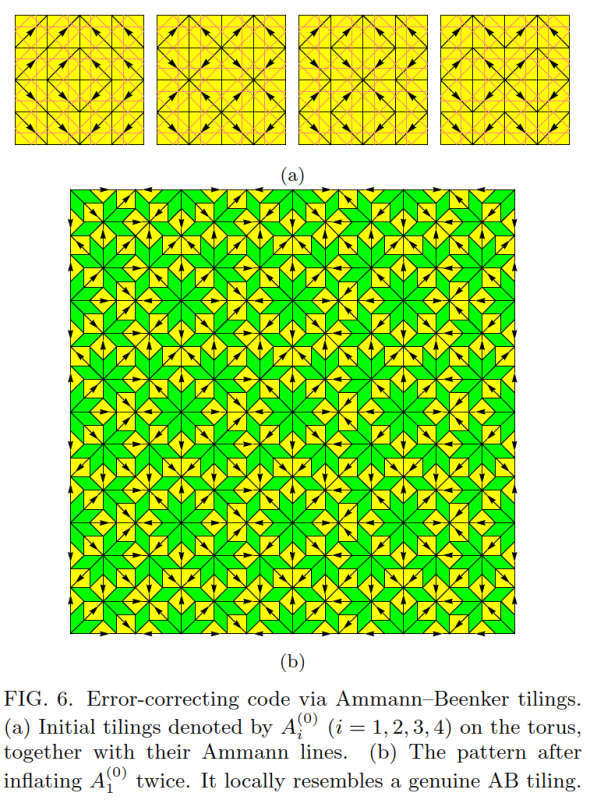
まず,図6(a)に示すように、トーラスの4つの「初期」タイリング$${A_{i}^{(0)} (i = 1, 2, 3, 4)}$$を定義する.タイリングは,トーラス上で切れ目のないまっすぐなAmmannバーを形成し,異なる方位の正方形が等しい頻度で現れるように設計されている.
次に,それらをABインフレーションルールをn回繰り返し適用し,4つのタイリング$${A_{i}^{(n) } }$$を得る.図6(b)に$${A_{i}^{(2) } }$$を図示する.簡単のために,各基本タイルのサイズを固定(各辺を1)すると,$${A_{i}^{(n) } }$$のサイズはnとともに指数関数で増加する.
興味深いことに,n≧2の$${A_{i}^{(n) } }$$は,トーラスのタイリングであり,局所的に本物のABタイリングに似ており,局所的に互いに区別できない.正確に言えば:
●半径$$ r_n=\Theta((1+\sqrt{2})^n) $$($${A_{i}^{(n) } }$$の線分サイズに比例)の内部にあるどのようなパターン$${A_{i}^{(n) } }$$も任意の本物のABタイリングに現れる.逆も成立.
●$${A_i^{(n) } }$$の中に半径$${r_n}$$のパターンの出現数はパターン自体にのみ依存し,iに依存しない.
証明は付録Dにある.
さて,以下の波動関数を構成することができる.
$${|Ψ_{i}^{(n)}⟩ ∝ \int dg|gA_{i}^{(n)}⟩}$$ (10)
ここで、トーラスの並進群上のgだけを積分します(回転も含めると、A3とA4
は等価になるからである)。
これらの波動関数$${|Ψ_{i}^{(n)}⟩}$$は、任意の半径rn
ディスクにまたがる。PT QECCの構成と同様に、これを検証するためには、ティリングが必要な局所的な
区別可能性と回復可能性の特性を持つことを確認すればよい。前者の性質は今説明した通りである。
後者はAmmann線から導かれる。
付録Eでは、第IV節と第V節のアイデアを組み合わせて、QECCを構成する。Vのアイデアを組み合わせて、有限かつ離散的なQECCを構築する。