Zh i Li and Latham Boyle:arXiv:2311.13040v2 [quant-ph] 25 Jan 2024 から抜粋し解説を加えた:
Penroseタイリング(PT)は,平面の非周期タイリングであり,多くの驚くべき性質を持つている.一方,量子誤り訂正コード(QECC)は,量子情報をノイズから保護する巧妙な方法である.PTとQECCとは全く関係がないように思うかもしれないが,この論文は,PTが注目すべき新しいタイプのQECCを生み出すことを指摘する.量子情報を 量子幾何学によって符号化するのだが,有限領域内(局所的)のエラーや消失は,領域がどんなに大きくても検出され修正できる可能性がある.
■ 緒言
Penroseタイリング(PTs) は,1970年代に発見された2次元平面のテッセレーションで,その美しく予想外の性質は,物理学者や数学者を魅了してきた.これらのタイリングは,本質的に非周期でありながら,完全な長距離秩序を持つ.自己相似性を持ち,周期的パターンでは禁止される10回対称性を持つ[訳者注)局所的,あるいは,ベクトル対称的な意味での10回対称].
1980年代に,これが準結晶の青写真であることも判明した.準結晶は,研究室でも,後に,自然界(太陽系の誕生,落雷,最初の原爆実験など)でも,存在が発見された.
量子誤り訂正符号(QECC)は,量子情報を高度な冗長性を用いて符号化する方法であり,ある種のエラーを検出修正し,元の量子情報を復元することができる.このようなコードは,物理学において,深く広範な役割を果たしている:・量子コンピューティン・凝縮系物理学・量子重力などの分野
PTとQECCは全く無関係に見えるかもしれないが,深いつながりがある.
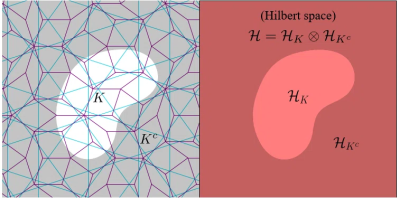
QECC側:量子エラー訂正の基礎となるのは,「回復可能性」(または訂正可能性)と「識別不能性」の間の等価性である:ある空間領域$${K}$$における任意のエラーと消失は,その領域が論理情報を含まない場合に限り訂正可能である;正確に言えば,コード空間の様々な状態が領域$${K}$$において識別不可能である場合にのみ符号化される.(量子情報は局所的領域ではなく,全域的な方法で符号化される)
PT側:「回復可能性」と「識別不能性」という類似の概念がある.
「識別不能性」:PTは実際には無限に存在し,それらは 全域的には等価でない(あるPTを平行移動したり回転させたりしても,他の異なるPTと全域的に一致させることはできない).全域的には等価でないが,局所的には識別できない.つまり,どのPTのどの有限パッチ(それが、どんなに大きくても)であっても,他のどの異なるPTにも出現しなければならない(どんなに大きな有限領域を探索しても,どのPTを探索しているのか判断できない).
「回復可能性」:PTの有限領域$${K}$$を消去した場合,その領域がどんなに大きくても,その欠損領域をタイリングの残りの部分(補空間領域$${K^c}$$)の知識から一意に回復できる.
PTの識別不能性と回復可能性の概念は,QECCのそれとよく似ている.ただし,前者は幾何学的配置に関する古典的な性質であり,異なる空間領域に関係するが,後者は符号化された量子状態(重ね合わせ量子状態を含む)に有効な性質であり,同じ空間領域内の異なる量子状態に関係する.
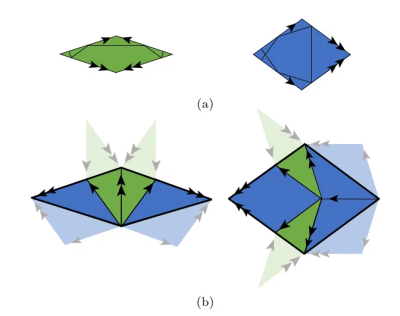
(a) Penroseタイリングを構成する2つの菱形,痩せた菱形(緑)と太った菱形(青). タイル内部に描かれた黒い線分がAmmann線. (b) Penroseタイリングのインフレーションルール.親菱形がインフレーションを起こすと,いくつかの子菱形の半分が生成される.この子菱形の半分は,隣接する親菱形のインフレーションによって生じる子菱形の半分(薄い色で示す)と組み合わされると親菱形と同じ菱形になる.
■「識別不能性」と「回復可能性」
上図のタイルの縁の矢,または,Ammann線によるマッチング規則は,PTを完全に決定するわけではない:
現実に数えきれない全域的に非等価なPTsが存在する.しかし,これらの非等価なPTは互いに密接に関連している.
数学的には,これらは局所的には識別できないという同じ類に属する:あるPT($${T}$$)に存在する任意の有限パッチは,他の任意のPT($${T^′}$$)にも出現しなければならない.したがって,絶対ユークリッド座標(原点の位置,$${\hat{x } }$$,$${\hat{y } }$$の方位)がなければ,非等価なPTはその「全域的な」振る舞いが異なるだけで,どんなに大きな有限領域を検査してもそれらを識別することはできない.
局所的識別不能性のより強力で定量的なバージョンは:$${T}$$のすべての有限パッチが$${T^′}$$に現れ,その逆も同様に成立するだけでなく,異なる有限パッチの相対的な頻度も同じである.実際,相対頻度はインフレーション・ルールからのみ計算できる.
もう一つの重要な特徴は,局所的な復元可能性である:任意の有限領域$${K}$$のパターンは,補空間領域$${K^c}$$のパターンから一意に復元できる.$${K^c}$$から$${K}$$へとAmmannバーを延長することができるため平面全体のAmmannバーを回復することができ,したがって,PT全体が回復できる.
■ QECCsの原理
保護したい量子情報は,ヒルベルト空間$${H_0}$$内の量子状態であるとする.QECCは,この量子状態を慎重に選択された冗長性とともに保存することで,ある種のエラーを識別し修正することができる.正確に言えば,"裸 "または "論理 "の量子状態のヒルベルト空間$${H_0}$$は,コード空間と呼ばれる慎重に選択された部分空間$${C}$$として拡大されたヒルベルト空間$${H}$$に埋め込まれることによって "符号化 "される.
本論文で扱う訂正可能なエラーは,任意の有限空間領域$${K}$$の消去で,結局,領域$${K}$$の任意のエラーは訂正可能である.
領域$${K}$$の消去が訂正可能であるのは,$${K}$$が論理情報を含まない場合,すなわち,符号空間$${C}$$の様々な状態が,$${K}$$において識別できない場合に限られるというのが基本的な事実[10, 11]である.Eq(1)参照.
空間領域$${K}$$は固定されていないことに注意しよう.空間全体を,それぞれがQECC条件を満たし,情報を含まない,このような多数の$${K}$$の合併に分解することができるから,QECCでは,量子情報は "全域的 "に保存される.
$${H}$$を$${H_{K}⊗H_{K^c } }$$と考えると(ここで,$${H_K}$$と$${H_{K^c } }$$は,領域$${K}$$と,補空間領域$${K^c}$$のヒルベルト空間である).識別不能性は次のようになる:
$${Tr_{K^{c } } |ξ⟩⟨ξ| = Tr_{K^{c } } |ξ^{'}⟩⟨ξ^{'}|}$$ (1)
$${^∀|ξ⟩ ,|ξ^′⟩∈C}$$は正規化されている(ここで、$${Tr_{K^c } }$$は$${H_{K^c } }$$のトレース).
空間$${C}$$が状態 $${|ψ_i⟩}$$で張られるとすると,式(1)は次の式と等価である.
$${Tr_{K^c} |ψ_i⟩ ⟨ψ_j| = ⟨ψ_j|ψ_i⟩ ρ_K}$$, $${^∀i, j}$$ (2)
ここで,$${ρ_K}$$($${H_K}$$の演算子)が$${i,j}$$に依存しないことが重要である.上記の基準では,$${\{|ψ_i⟩\} }$$は正規化されていないか,直交していないか,あるいは過完備である可能性がある.証明は付録Aを参照.
保護される状態 は "基底 "状態$${|ψ_i⟩}$$に限定されないで,任意の重ね合わせ量子状態($${C}$$の任意の状態)でよいことを強調しておく.
このような背景を踏まえて,任意の有限空間領域$${K}$$で任意の消去とエラーを訂正することのできるPT QECCを構築する準備が整った.
■ Constructing the PT QECC
ペンローズ・タイリングの集合$${\bar{T } }$$ を考える.$${T}$$ が$${\bar{T } }$$中の特定のPTを表すとすると,$${gT}$$は,$${T}$$から2次元ユークリッド変換(平行移動、回転)によって得られるPTを表す.
$${[T]=\{gT\} }$$は,"2次元ユークリッド変換で$${T}$$に等価なすべてのPTの類を表す.
タイリング$${T}$$は,量子力学的ヒルベルト空間$${H}$$の状態$${|T ⟩}$$とみなすことができる.
平面$${R^2}$$を任意の空間領域$${K}$$と補空間領域$${K^c}$$に分割すると,タイリング$${T}$$はそれぞれ$${K}$$と$${K^c}$$内の対応する部分$${T_K}$$と$${T_{K^c } }$$に分割される.
これはヒルベルト空間 $${H=H_K⊗H_{K^c} }$$の分解と,それに対応する状態$${|T⟩=|T⟩_{K}|T⟩_{K^{c} } }$$を導く.
ここで,$${|T⟩_K ∈H_K}$$と$${|T ⟩_{K^c}∈H_{K^c } }$$は,それぞれ$${T_K}$$と$${T_{K^c } }$$にのみ依存する.
2つのタイリング$${T}$$と$${T^′}$$が異なる場合(異なるとは,絶対座標系が存在する場合に異なるという意味であり,全体的なユークリッド変換によって異なるだけの2つのタイリングでさえも,一般的には異なる),それらは$${H}$$における直交状態によって表される.
$${⟨T^{′}|T ⟩ = δ(T^{′}, T)}$$ (3)
同様に、$${K}$$において$${T}$$と$${T'}$$が異なる場合
($${ T_{K} \ne T^{'}_{K } }$$),$${ |T⟩_K }$$と$${ |T^{′}⟩_K}$$は$${H_K}$$において直交する.
各同値類$${ [T]}$$に対して,波動関数が定義される
$${|Ψ_{[T]}⟩ =\int dg |gT⟩ }$$, (4)
ここで,すべてのユークリッド変換 $${g}$$ を重ね合わせるので,
$${|Ψ_{[T]}⟩}$$は$${[T]}$$にのみ依存する.図3参照.
この論文の主たる主張は,状態$${ |Ψ_{[T]}⟩}$$は,任意の有限領域$${K}$$でエラーや消去を訂正するQECCのコード空間$${C\subset H}$$の直交基底を形成することである.
図3 波動関数Eq(4)のイラスト.
(無限)Penroseタイリング$${T}$$が与えられたとし,右辺の各項は$${gT}$$によるユークリッド変換バージョンを表現している.同一タイリングを並進や回転させた変換$${gT}$$'sの中から4つのパッチが描かれている.
$${⟨Ψ_{[T]}|Ψ_{[T']}⟩=0}$$, if $${[T]\ne [T']}$$のとき
$${Tr_{K^{c } }|Ψ_{[T]}⟩⟨Ψ_{[T′]}|=0}$$, if $${[T] \ne [T]}$$のとき
$${=⟨Ψ_{[T]}|⟨Ψ_{[T]}⟩\rho_{K } }$$, if $${[T]=[T']}$$のとき (5)
Eq(5)の始めの条件は,幾何学的PTの回復特性から得られる.Eq(4)に注意すると,$${ Tr_{K^{c } }|Ψ_{[T]}⟩ ⟨Ψ_{[T′]}|}$$が消えるのは,2つの古典的配置$${T,T'}$$(異なる類に属する$$ [T]\ne [T ′] $$)が$${K^c}$$上で異なる必要がある.言い換えれば,$${K^c}$$での配置は,それが属する同値類で一意に決定される.これはPTの回復可能性で保障される.
Eq. (5)の2番目の条件を調べるのに,明示的な計算をしよう:
$$ Tr_{K^c} |Ψ_{[T]}⟩ ⟨Ψ_{[T]}| =\int \int dg′dg δ(gT, g′T) |gT⟩_{K}⟨g′T |_{K}=\int dg′′ δ(T, g′′T ) ·\int dg |gT⟩_{K}⟨gT|_{K} . $$ (6)
ここでも,最初の等式は PT の回復可能性による.$${Tr_{K^c} |gT⟩ ⟨g′T |}$$が非ゼロになるためには,$${gT}$$ と$${g'T}$$ が $${K^c}$$ で一致し,したがって全域で一致する必要があり,デルタ関数が得られる.$${δ(gT, g'T)}$$ は差 $${g'' = g^{−1}g'}$$ にのみ依存するため,2 番目の等式が続く.
因子$$ \int dgδ(gT, T) $$は,次のように$$ ⟨Ψ_{[T]}|Ψ_{[T]}⟩ $$に比例することに注意せよ.
同じ引数であるため,$${ρ_{K,[T]} =\int dg |gT⟩_{K} ⟨gT|_{K } }$$ が実際には$${T}$$に独立であることを示すだけで十分だ.
これはまさに PT の局所的識別不能特性である.実際,$${ρ_{K,[T] } }$$ は,$${K}$$ を回転および平行移動することによって$${T}$$ に現れる可能性のあるすべての局所パターン $${T_K}$$ の古典的な混合物であり,相対頻度によって重み付けされている.
局所的な識別不能性、つまり局所パターン $${T_K}$$ (相対頻度を含む) がすべてのタイリング $${T}$$ で同じであるということは,$${ρ_{K,[T] } }$$ が $${T}$$ に依存しないことを意味する.
要約すると,Penroseタイリングの特性を利用することにより,任意の有限領域内の任意のエラーと消去を訂正できる QECC を構築した.このコードでは、コード空間 $${C}$$ で各基底状態$${|Ψ_{[T]}⟩}$$ が,同値類$${ [T]}$$ 内のすべてのタイリング $${|T⟩}$$ に対する量子重ね合わせで,典型的なコード状態は,そのような基底状態(つまり,異なる同値類$${ [T ], [T'],...}$$)の量子重ね合わせとなる. したがって,量子情報はPenroseタイリングがどのように重ね合わされるかという量子幾何学構造にエンコードされる.