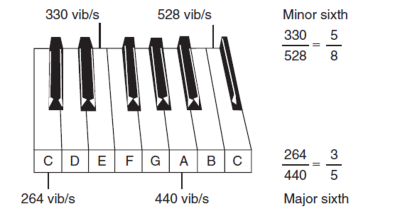
音は空気の振動で,音の高低は振動数(周波数)で決まります.音楽で使う音は,周波数の(離散的に)決まった幾つかの音です.つまり,2つ以上の音が快く調和して聞こえるのは,構成要素であるそれぞれの音の周波数の比ができるだけ簡単な整数比であることが必要で,そのような音の集合の中を音の高さ(周波数)の順に並べたものが音階です.2つの音の周波数比が最も簡単なのは,2倍あるいは1/2倍で,そのような2つの音の比は「オクターブ」といいます.1オクターブの中に半音12個の音を選ぶと,それらから選んだ2音の周波数比ができるだけ簡単な整数比になるようにできました.これが音階で,これは大変な発明だったと思います.単音の集合としての音階を次の2つの公理を満たすとして,数学的に定義しましょう:
音階の中に周波数 $${f}$$ の音が存在すれば,周波数 $${2f }$$と $${f/2}$$ の音は常に音階に存在する.(オクターブの存在)
任意のメロディーを,音階中の任意の音から始めることができる.(移調が可能)
このような2つの公理で定義された音階は,平均律といいます.平均律音階{$${f_n}$$}は,公比$${q}$$(半音階)の等比数列であることがわかります.
2音の周波数比が簡単な比であれば純粋な和音になりますが,厳密にいえば,平均律にはオクターブ以外に純粋な和音はありません.つまり,平均律音階の音はオクターブ以外は,簡単な比というのは近似的なことで,厳密ではありません.完全5度 (全音3つと半音1つ)とは,周波数比が 3/2 の 2 音のことで,例えば,C(ド)-G(ソ),G(ソ)-D(レ),D(レ)-A(ラ),A(ラ)-E(ミ)などの間隔です.純正律ではこれらの周波数比は3/2にできます.
1オクターブは12の半音で構成されますから,平均律では$${q^{12}=2}$$,すなわち,$${q=2^{1/12}=1.0595}$$ [2の12乗根]で,$${q}$$は半音に相当する公比. 平均律の完全5度音程の周波数比は $${q^7}$$です.したがって,平均律の完全5度では $${q^7=2^{7/12}=1.4983...≠3/2}$$ となり,純正律の3/2=1.5 とは,ほんのわずかですが違います.
同様に, 完全4度(全音2つと半音1つ)の音程,例えば,E(ミ)-A(ラ),A-D,D-G,G(ソ)-C(ド),C-F,B-Eの周波数比は,純正律では4/3にできますが,平均律では4/3とわずかに異なります:$${q^5=2^{5/12}=1.3348...≠4/3}$$.4/3=1.3333ですから,この差もほんのわずかです.
バイオリンには,G,D,A,Eの4弦があります.調律はA線を440(あるいは442)Hzに合わせた後,それぞれの弦を完全5度の間隔に合わせるので,純正律になっています.
ギターは最も低い第6弦Eから第3弦Gまでと,第2弦Bと第1弦E間を完全4度の間隔に,第3弦と第2弦間は長3度に調弦するそうですが,純正律をつくれます.
1オクターブを12 のステップに均等分割することは,ピアノの鍵盤を作るには必要で,ピアノは平均律ですが,平均律は純正律の非常に良い近似になっています.
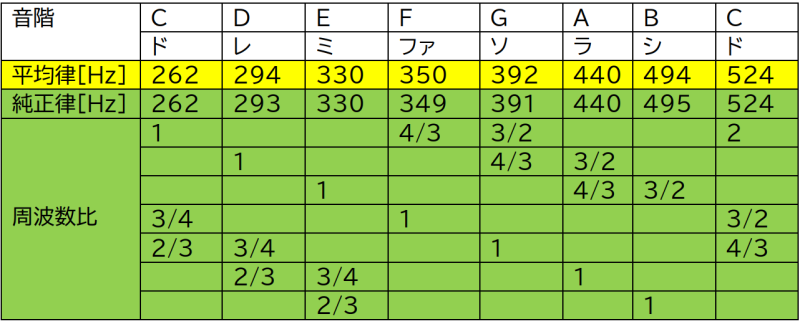
以下の表の純正律の音の周波数は,オクターブ,および,完全5度と完全4度の音程が簡単な整数比にするという条件で計算しました.
-----
参考文献
https://note.com/sgk2005/n/nc5534e950cfa
https://www.mathedu.ru/files/news/books/matematicheskaya_sostavlyayushhaya_2019.pdf
http://www.enjoy.ne.jp/~k-ichikawa/junseiritsu.html