理論を実用にすること.別の分野でも同じ式が現れること.
Алексей Николаевич Крылов; アレクセイ クリロフ
Прикладная математика и техника / Статьи — Математическая составляющаяより◆
19世紀の第1四半期には,このような数学の物理学への応用が発展した:ポアソン,コーシー,イギリス人グリーンの研究などがその例だ.
ポアソンの一見純粋な理論的な研究が,40年後に航海の安全に多大な貢献をした重要な実用応用の基礎となった.
1824年,ポアソンは磁気の数学的理論に関する膨大な研究の中で,船上の羅針盤コンパス(方位磁石)の平衡に関する一般方程式を与えた.
ポアソンは,船の固定具と武装の鉄によるコンパスへの摂動効果を考慮して,船のコンパスの指針の平衡のための一般的な方程式を与えた.
これらの方程式は,与えられた船に関する12の定数係数を含んでいた.
ポアソンは,この係数を決定するための実用的な方法は何一つ明示しておらず,純粋に理論的研究にとどまっていた.
物理学者にとっては,これらの方程式は何の興味もなく,船乗りにとっては,アクセス不能であり理解不能であった.そして,この有名で多作な著者の400の論文の一つに埋もれてしまっていた.
ただ天文学者のエリーだけが,ポアソンの考察を用い,磁石と鉄の棒をコンパスの近くに特定の方法で置くことによって,コンパスに船の鉄と反対の効果をもたらす(つまりコンパスの偏差を消す)簡単な方法を示した.しかし,ある場所で消された偏差は,船が他の場所を通過すると再び現れた.
1841年に亡くなったポアソンの時代には,船は木造で,鉄は比較的少なくその影響は小さく,コンパスの偏差は他の誤差に吸収されていた.
しかし 1840 年代半ばから,鉄製造船と蒸気船が発達し始め,急務の定期航路が確立され急速に発展した.1862年には1ヵ月も経たないうちに,アメリカ航路を担っていた2隻の大型客船がアイルランド沖で相次いで沈没し,貴重な積荷に加えて,数百人が命を落とした.
調査の結果,沈没の主原因のひとつは,船舶の航行計画の誤りであることが判明した.コンパスの読みに誤りがあり,そのために船が進路を誤ったのである.
イギリスの世論は警戒を強め,議会の要請を受けた提督は,数学者のアーチボルド・スミス,天文学者のエリー,エヴァンス大尉を含むコンパス委員会を結成した.
彼らは,ポアソンの方程式を蘇らせ,使いやすいように変換した. つまり,教育を受けた船乗りなら誰でも利用できる,実用的な提督用のコンパス偏差マニュアルが出版されたのである.
当時,ロシア初の戦艦がイギリスで建造中であった.I.P.ベラベネツ大尉が指揮する戦艦砲台「ペルベネツ」であった.彼は,特に,旧式化した戦艦に代わる戦艦の建造が始まったという事実を考慮して,航海のためのコンパスの偏角の教義の重要性を学んでいた.
特に,当時,時代遅れの木造船に代わって装甲軍艦の建造が始まっていたことを考えれば,航海のための羅針盤の偏角の重要性は明らかであった.
彼の提案でコンパス観測所がクロンシュタットに設立され,船員で優れた数学者であったI.P.デ・コロングがベラベネツの助手に任命された.
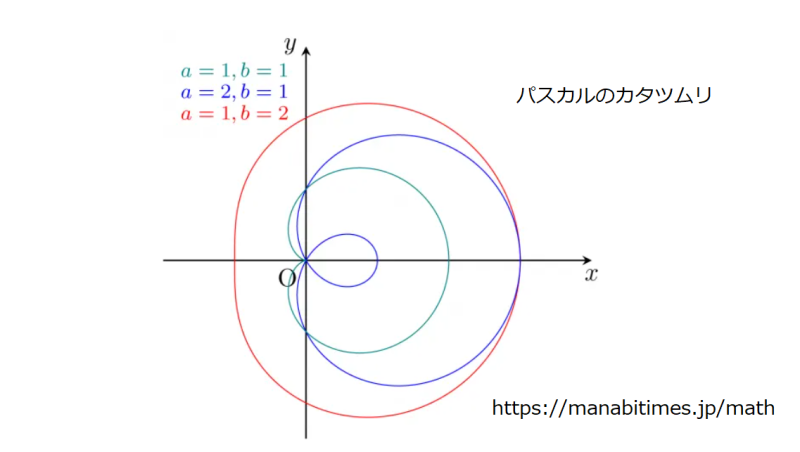
コロングは,1640年代にパスカルによって発見された「パスカルのカタツムリ」と呼ばれる曲線の性質を利用することで,コンパスの偏差理論に大きな進歩をもたらした.
磁力を測定し,偏差を消すための多くの機器を発明し,コンパスを改良した.これは今でも世界最高のものである.
この典型的な例は,抽象的な理論的研究が技術や実践に影響を与え,浸透していることを特に明確に示している.有名な著者が理論的な正当性を示すが,詳細や特殊性には踏み込まない.十分な訓練を受けた知識豊富な専門家が彼の理論を理解し,それを実用的で適用可能な形にする. 実践的で応用可能な形を与え,その結果を生活に,技術に応用する.
この例を上げたのは,私は1884年から数年間,I.P.ド・コロングの最も身近な助手兼弟子として働いており,彼が造船という大きな仕事に移るまで,コンパスの偏差の理論と偏差を消す実践を徹底的に研究していたからである.
別の例もある.有名な天文学者であり数学者であったガウスは,1833年にいわゆる絶対測度系を確立した.これにより,当時は純粋に科学的な関心事であった磁気と電気の現象が,機器や観測者に依存しない正確で明確な測定対象となった.その45年後,電気工学という新しい技術分野が誕生し,電気計測は実用上非常に重要なものとなった.
さらに45年が経ち,どんな都市でも,やがてどんな村でも 田舎で電気メーターがない家はない.もちろん,これらのメーターを作ったのはガウスではない.おそらく彼はそれらを考えたこともないが,その基礎は彼の天才によって築かれたのである.
ガウスは,1822年には,デンマーク科学アカデミーが提示した地図のネットワーク構築に関する懸賞問題に一般解を与えた.それから90年後,物体の上を流れる液体の運動や,飛行機の翼の上を流れる空気の運動で,まったく同じ問題に直結することが判明した.
熱伝導の問題は,1808年にはフーリエによって解決されていたが,50年後,W.トムソンの手によってこの本格的な応用が始まった.
ケルビン卿が,大西洋に最初の電信ケーブルを敷設したとき,最初はうまくいかなかった上に,電信はつながったものの,モールス信号のドットやダッシュのような単一信号が8分間も続くのだった.
W.トムソンは,1808年に発表されたフーリエの方程式と1828年に発表されたグリーンの方程式から,ケーブルを稼働するために何をしなければならないかを読み取ることに成功したが,それを読み取るにはウィリアム・トムソンでなければならなかった.
現在,電気計測の方法は,熱計測の方法とは比較にならないほど単純で正確であり,同時に冷凍も発達している,
冷蔵船は大きく発展した.冷蔵室の断熱の配置は,数学的分析に適さないだけでなく,直接経験することさえできないような問題を提起する.
しかし,電気測定によって,熱流線ではなく電流線を調べることで,計算に必要なデータを得ることができる.この研究は現在 科学アカデミーの物理数学研究所で行われているが,すべての技術計算の背後には,数十万から数百万ルーブルの費用がかかることを忘れてはならない.
全く異なる分野の問題でありながら,同じ動的微分方程式が現れるこのようなアナロジー例はたくさんある.太陽に引き寄せられる天体運動の計算と,波打つ船の揺れとの間に,あるいは,天体運動におけるいわゆる長年の不平等の決定と,船のプロペラや発電機のために働く多気筒ディーゼルエンジンのシャフトの最大振動との間に,共通点があるように思われる.
方程式は同じだから,数式や方程式を書くだけでは,どちらの問題を解いているのかわからない.エンジニアは,多くの問題の解決に応用される一般的な数学的手法をマスターしなければならない.
今日では,建設,造船,航空機製造,砲兵,電気工学,光学など,あらゆる工学分野の技術に数学が浸透しており,事前に計算されていない建設物は想像だにできない.工場の研究所や技術局の従業員には数学者がいる.これらの研究所の機関誌には,技術的な研究とともに,これらの研究所の職員による純粋に数学的な研究が掲載されることが多い.このように,最も重要な道具としての技術と数学の結びつきははっきりと認識されている.
これらの例によって,数学の技術への応用の重要性は十分に明らかになったが,数学は,古代ギリシャの哲学者たちによって築かれた道,すなわち,純粋な思索,純粋な論理を,それ自身によって創造された抽象的な対象に適用し,その性質と量的関係を研究し,推論と証明の絶対的な厳密さと不変性を何よりも追求する道筋に沿って,独自の発展を続け,100年前のコーシーとポアソンの研究によって築かれた道筋よりも,ここ50~60年の間にはるかに発展してきた.
それゆえ,数学とテクノロジーの間には,またしても一見不和がある.数学は技術者に必要なものを与えない.しかし多くの場合,それは技術者が自分の疑問に対する答えを探す場所を間違えているからである.
それゆえ,技術者が,数学が切り開く無限の素材の中で,どのような選択ができるのか,と問うのは自然なことである.
最も単純な答えは,この問いをもう少し深く掘り下げれば出てくる.
どんな技術的な努力においても,重要なのは,結論や結果に至る論理的な過程ではなく,結論や結果そのものなのである.
"数と尺度 "で表現され,したがって,方程式を立て,それを最後まで解く,計算を簡略化する,数学的な問題を解く近似的な方法を適用する,といった意味で数学が与えるものすべてが重要なのである. 数学的な問題を解くための方法は,その方法が使われた問題とは何の共通点もないような問題にも,遅かれ早かれ使われ,しばしば適用されることになる.
1814年当時,複素関数の理論以上に抽象的なものがあっただろうか.それから100年後,コーシーがこの理論の基礎を示した後,ジューコフスキーとチャプリギンは,この理論を形状決定や飛行機の翼の正確な計算に応用した.よく研究されたさまざまな関数の表は,膨大な労力の結果である.
このような表は,編纂者の多大な労力の賜物であり,未来のすべての世代を無駄な労働から救う宝物である;
技術者は,どのような関数が研究されているのか,そのためにどのような表があるのかを知っていなければならない.