GPSやGLONASS(ロシアの衛星測位システム)受信機が,軌道上の衛星から座標を受信すると考えるのは間違っている.第一,衛星はあなたの座標を知らないし,第二に,衛星はメッセージを,あなただけでなく全員に,一斉に「宇宙から」送信している.では,ナビゲーターはどうやってあなたの座標を決定するのでしょうか?衛星ナビゲーション・システムには,宇宙と管理の2つの主要機能がある.宇宙機能は,地球の周囲に均等に衛星を配置することである.地球上にある管理機能は,すべての衛星で「システム全体」の時刻を同期させ,単一の座標系を使用することを保証する.各衛星は,メッセージ送信時の衛星の座標と送信時刻を含むナビゲーションメッセージを継続的に送信している.このようなメッセージを受信した受信機は,衛星までの距離を次のように計算することができる:$${d =(t^{(pr)} - t^{(otpr)})c}$$この式では,信号の移動時間(送信時刻$${t(otpr)}$$から受信時刻$${t(pr)}$$まで)に無線信号の伝搬速度,すなわち光速$${c}$$を乗じている.一方,直交座標系であなたの座標を$${(x; y; z)}$$とし,送信時の衛星の座標を$${(x1; y1; z1)}$$とすると,衛星とあなたの距離$${d_1}$$の2乗は$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2}$$である.受信機が同時に2つの衛星からナビゲーションメッセージを受信した場合,受信機はあなたの座標$${(x;y;z)}$$を求めることができる.
$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2 =d_{1}^2}$$
$${(x - x_2)^2 +( y - y_2)^2 +(z - z_2)^2 =d_{2}^2}$$
$${(x - x_3)^2 +( y - y_3)^2 +(z - z_3)^2 =d_{3}^2}$$
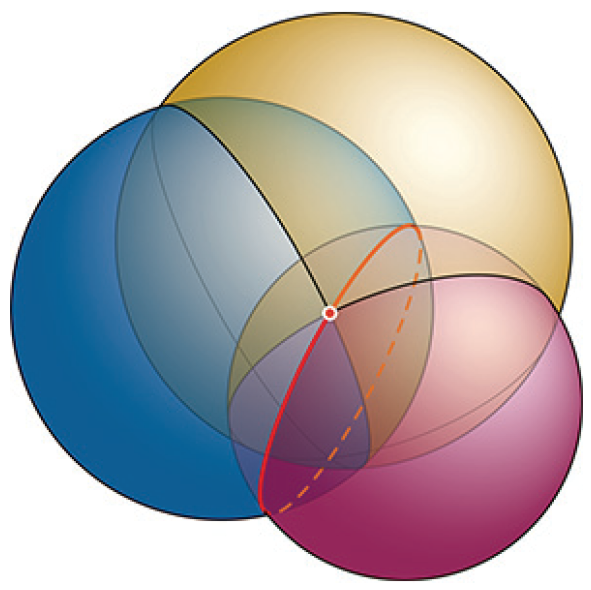
ここで,$${(x_i; y_i; z_i)}$$は$${i}$$番目の衛星の座標で,$${d_i}$$は衛星までの距離である.このシステムの幾何学的解釈は以下の通りである.ある衛星からのメッセージ は,あなたがいる地点を中心とし,衛星までの距離を半径とする球を定義する.
これら2つの球体の交点は,一般的に言えば円である.第3衛星からのメッセージはもう1つの制約(もう1つの球)を追加する.それらにより,あなたの座標は決定される.3つの球が共通の点を持つということは,システムの構成そのものから導かれる.2つの「形式的な解」(円と3つ目の球の交点)のうちの1つは題意に適さず,もう一つがあなたの座標である.記述した衛星 ナビゲーションシステムのスキームは単純化されているが,現実にはもっと複雑なモデルを使う必要がある.例えば,記述された方式は誤差に非常に敏感である.主要な誤差の一つは,時計の精度の影響である.
衛星の時計はナビゲーション・システムの地上局と通信し時間を修正する手段を持たない.もし,時計がシステム全体の時刻と0.001秒ずれているとする.光速は秒速30万キロメートルであるので,衛星までの距離に300キロの誤差が生じる!記述したシステムでは,もし解があったとしても,あなたの場所は違うものになるだろう.幸いなことに,このような問題も克服可能である.たとえ時計の精度がわからない,例えば,受信機の時計がシステム全体の時刻より(未知の)$${δ}$$だけ遅れているとしよう.メッセージを受信した瞬間の読みは$${t^{(pr) } }$$である.ナビゲーターは,衛星までの距離を$${d =(t^{(pr)}-t^{(otpr)})c}$$と「仮定」する.これは真の距離$${d +δc}$$より小さい.座標$${(x; y; z)}$$と新しい未知数$${r =δc}$$を求めるには,別の方程式が必要である.4つの衛星からのデータがある場合に次のようなことができる:
$${(x - x_1)^2 +( y - y_1)^2 +(z - z_1)^2 =(d_1 +r)^2}$$
$${(x - x_2)^2 +( y - y_2)^2 +(z - z_2)^2 =(d_2 +r)^2}$$
$${(x - x_3)^2 +( y - y_3)^2 +(z - z_3)^2 =(d_3 +r)^2}$$
$${(x - x_4)^2 +( y - y_4)^2 +(z - z_4)^2 =(d_4 +r)^2}$$
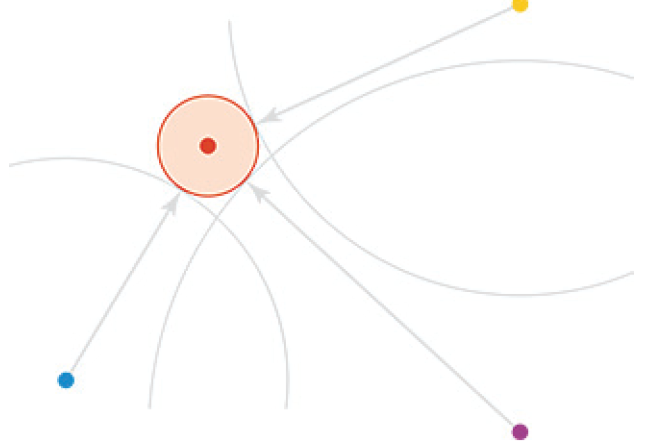
この問題の解を幾何学的に解釈すると次のようになる.受け手は半径$${r}$$の球の中心であり,その球は外部から(時計が遅れていたため)半径$${d_i}$$の4つの球に接しており,その中心は衛星である.このような球が存在し,その中心があなたの位置である.(図はこの問題の2次元バージョンを示している.半径$${r}$$の円が3つの円に外部で接している).このシステムを使って座標を計算することで,ナビゲーターは,座標が得られ,追加の "ボーナス "として,ナビゲーターはシステム全体の時間の値を受け取り,時計を修正し,正確な時刻をあなたに伝えます!
応用:ナビゲーション・デバイス
数学: 球、座標法、方程式系
『数学的構成要素』p.110-111より
2次元の世界のGPSなら2つの衛星,3次元の世界のGPSなら3つの衛星が最低必要だということです。