数学月間(第1日目)の講演の1つ[2024.7.22,13:40-15:10]は,「差分法を通じて眺める連続と離散」齊藤宣一(東大数理科学研究科)でした.
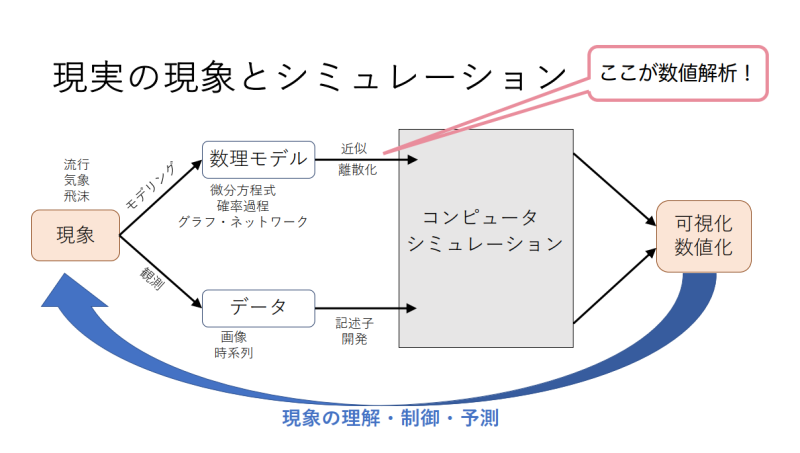
人類最初の微分方程式は,I. Newton(1642-1727)による惑星運動の方程式でした.その後,流体力学,固体力学,電磁気学などで,現実現象を記述する微分方程式が,次々に発見されました.熱伝導方程式,波動方程式,Navier-Stokes方程式などです.しかし,それらを解くことは簡単ではなかった.近代的なコンピュータの発明により,実際に,これらの微分方程式を解くことができるようになり,これが私たちの生活を豊かにしています.
■熱方程式(熱伝導方程式)
針金の温度: $${u(x,t) (0\leq x\leq 1, t\geq 0 )}$$$${\displaystyle \frac{ \partial u}{ \partial t}=\displaystyle \frac{ \partial ^{2}u}{ \partial x^{2 } } }$$境界条件: $${u(x,t)=0 (x=0,1)}$$
この方程式はFourierの方法で,以下の解析解が得られることが分っている.$${u(x,t)=\displaystyle \sum_{n=1}^{ \infty }2\left( \displaystyle \int_{0}^{1}u(x,0)\textrm{sin}(n\pi y)dy \right) e^{-k(n\pi )^{2}t}\textrm{sin}(n\pi x)}$$
差分法による解法
●差分商-----------------------------------------------------------------------------
$${\displaystyle \frac{df}{dx}(a)=\displaystyle \frac{f(a+h)-f(a)}{h}, \displaystyle \frac{f(a)-f(a-h)}{h } }$$
$${\displaystyle \frac{df}{dx}(a)=\displaystyle \frac{f(a+\displaystyle \frac{h}{2})-f(a-\displaystyle \frac{h}{2})}{h } }$$
$${\displaystyle \frac{d^{2}f}{dx^{2 } }(a)=\displaystyle \frac{1}{h}\left( \displaystyle \frac{f(a+h)-f(a)}{h}-\displaystyle \frac{f(a)-f(a-h)}{h} \right) =\displaystyle \frac{f(a-h)-2f(a)+f(a+h)}{h^{2 } } }$$
------------------------------------------------------------------------------------
$${U_{i}^{n}=u(i \Delta x, n \Delta t)}$$を用い,連続である熱方程式を差分方程式に直すと,
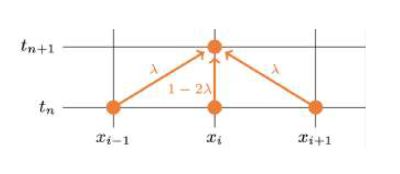
$${\displaystyle \frac{U_{i}^{n+1}-U_{i}^{n } }{ \Delta t}=\displaystyle \frac{U_{i-1}^{n}-2U_{i}^{n}+U_{i+1}^{n } }{ \Delta x^{2 } } }$$
$${\lambda =\displaystyle \frac{ \Delta t}{ \Delta x^{2 } } }$$と置くと,
$${U_{i}^{n+1}=(1-2\lambda )U_{i}^{n}+\lambda (U_{i-1}^{n}+U_{i+1}^{n})}$$ が得られる.
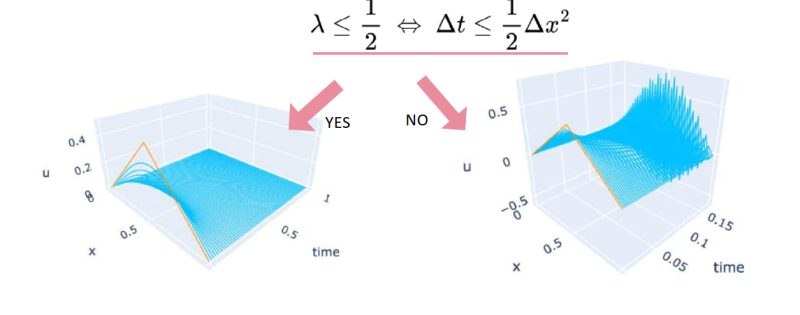
実際,計算してみると $${\lambda \le \displaystyle \frac{1}{2} \Leftrightarrow \Delta t \le \displaystyle \frac{1}{2} \Delta x^{2 } }$$ が必要であることが分る.
$${\lambda\leq 1/2}$$は,時間に関する差分解の安定性を保証している.
[証明]$${|u_{i}^{n+1}| \le (1-2\lambda )|u_{i}^{n}|+\lambda (|u_{i-1}^{n}|+|u_{i+1}^{n}|), (1 \le i \le N)}$$であるから, $${\displaystyle \max_{1\leq i \leq N}|u_{i}^{n+1}|\leq \max_{1\leq i \leq N}|u_{i}^{n}|}$$,従って,$${\displaystyle \max_{1\leq i \leq N}|u_{i}^{n}|\leq \max_{1\leq i \leq N}|u_{i}^{0}|}$$が成立する.
精密な解を得るには,$${\Delta x \longrightarrow 0, \Delta t \longrightarrow 0}$$とするのだが,$${\lambda \le \displaystyle \frac{1}{2} \Longleftrightarrow \Delta t \le \displaystyle \frac{1}{2} \Delta x^{2 } }$$の条件は,空間刻み幅に対して時間刻み幅を十分に小さくしなければならないことを意味する.$${ \Delta t=\alpha \Delta x^{2 } }$$に従って細分化すると,結果は正しい解に収束するが,$${ \Delta t=\beta \Delta x}$$に従って細分化すると,発散(実害はない)することも,別の解に収束(誤りに気付かない)することあり,数学理論を踏まえての計算が必要な所以である.
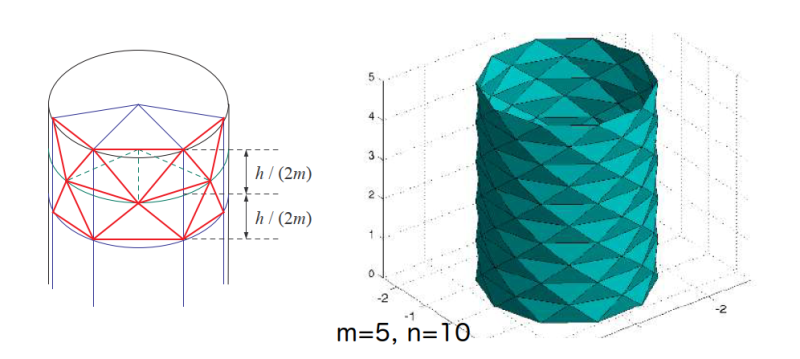
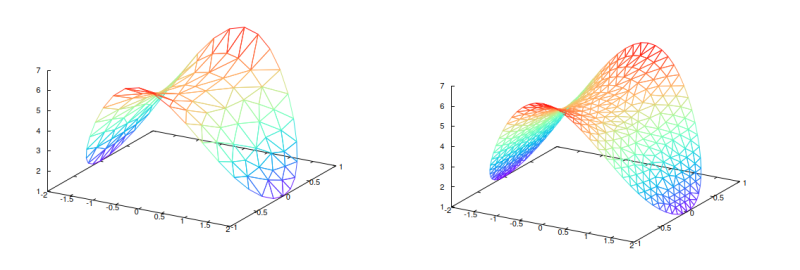
■三角形分割を限りなく細かくすることで,曲面の面積を求めることは出来るだろうか.
●円柱の側面積を求める
シュワルツの提灯
●『解析学序説』下巻;一松信(1964)p.119 より引用----------------
この立体を仮にシュワルツの提灯とよぼう.・・・$${m=n→∞}$$にすれば,期待の値$${2\pi rh}$$に収束するが,$${m=n^2→∞}$$とすると,$${2\pi r \sqrt{h^2+r^2\pi^4 } }$$という妙な値になり,さらに$${m=n^3→∞}$$とすると$${∞}$$になってしまう.よく考えてみればこれは当然かもしれない.$${n}$$に比べて$${m}$$をものすごく多くすれば,小三角形は激しく波うち,見掛け上狭い範囲に,おびただしい面積をもつ面がおりたたまれていることになる(提灯という名前はこれからつけた).
-------------------------------------------------------------------------------------------
ラーデマッヘル(H. Rademacher)の条件 (1919, 1920)
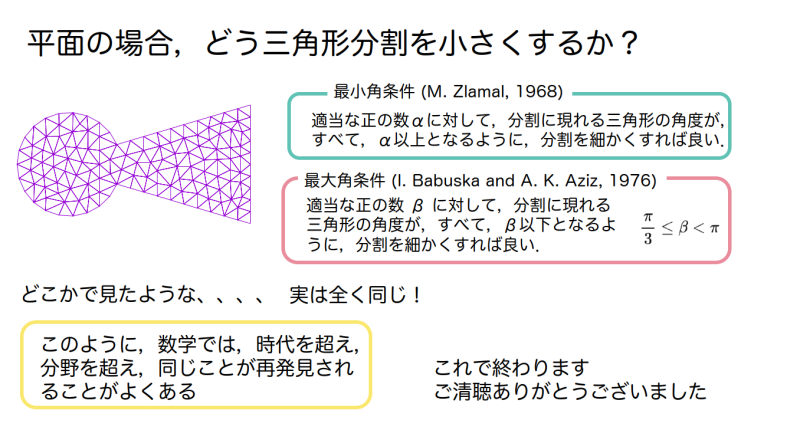
適当な正の数αに対して,分割に現れる三角形の角度が,すべて,α以上となるように,分割を細かくすれば良い.これは,分割を細かくする過程において,三角形がつぶれないことを要請している.
ヤング(Young)の条件 (1921)
適当な正の数 β に対して,分割に現れる三角形の角度が,すべて,β以下となるように,分割を細かくすれば良い.$${\pi/3\leq \beta \leq\pi}$$最大角が π に近づかないことを要請しているので,結果的に,三角形がつぶれないことを要請している.
どのように三角形分割をすれば良いかについて上記2つの条件が知られている.
■有限要素法について
・計算対象を,三角形・四面体に分割し,各四面体上で,近似方程式をたてて,それを統合し,近似解(数値解)を得る.• 普通,連立一次方程式を解くことに帰着される.未知数の数は,$${10^{10 } }$$程度になることも.• 有限要素法で,正しい解が得られるかどうかを研究するのは,数学の一つの役割である.• 問題が,平面問題なら,計算対象を三角形分割する問題がでてくる.