以下のサイトにある問題をグラフを使い解いてみましょう:
https://tomari.org/main/java/senkeikeikaku.html 線形計画(シンプレックス法)
ある会社が、A、Bという製品を売り出している。 それらを製作するための材料はプラスチック、アルミ、ゴムである。
それぞれ1個を製作するために必要な材料の量は下の表のとおりである。
このとき、手持ちの材料の範囲内で売上高を最大にするためには、A、Bをそれぞれいくつ作ったらよいか?
製品Aを$${x}$$個,製品Bを$${y}$$個作るとする.
この時の売上高を評価関数$${f(x,y)}$$にし,これを最大にする$${(x,y)}$$を求める.
$${f(x,y)=2x+3y}$$
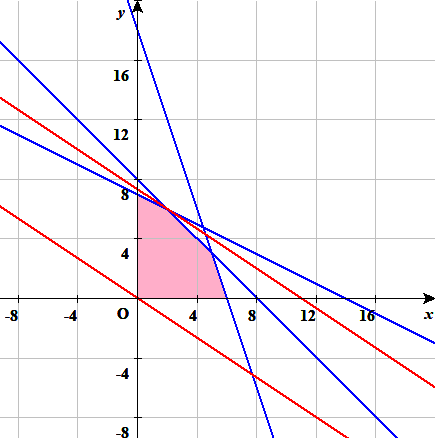
可能集合(可能領域)は,以下の制約条件で決まる
$${x+2y≦14}$$ , $${x+y≦8 }$$ , $${3x+y≦18}$$, $${x≧0}$$, $${y≧0}$$
可能領域を囲む頂点は,5つあるが,可能領域外頂点は5つである.
領域は凸多面体であるので求める極値は頂点にあり,
$${(2, 6)}$$のとき,最大値$${f(x,y)=22}$$となる.
行列表現
これを $${A=\left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right)}$$, $${x=\left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right)}$$, $${b=\left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right)}$$, $${c=\left( \begin{array}{@{\,} c @{\, } } 2 \\[0mm] 3 \end{array} \right)}$$ と表現すると,
制約条件は $${Ax≦b}$$となり,$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$
この制約条件下で,$${c^{T}x}$$を最大にする$${x≧0}$$を求める問題である.
$${x≧0, Ax≦b}$$のもとで, $${c^{T}x}$$を最大とせよ.
$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$
$$\left[ \begin{array}{@{\,} ccccc @{\, } }
1 & 2 & -1 & 0 & 0 \\[0mm]
1 & 1 & 0 & -1 & 0 \\[0mm]
3 & 1 & 0 & 0 & -1
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
z_{1} \\[0mm]
z_{2} \\[0mm]
z_{3}
\end{array} \right] \le \left[ \begin{array}{@{\,} c @{\, } }
4 \\[0mm]
8 \\[0mm]
18
\end{array} \right] $$
この例題は,2次元(2変数)の例題であるが,問題を一般化して$${n}$$次元の問題が考えられる.
■$${n}$$次元の問題に対するDantzigのアルゴリズム
可能集合の1つの頂点を選ぶ.
可能集合の辺に沿って頂点から頂点へ移る.
普通,頂点には$${n}$$本の辺があるが未知の最適解に近づく方向を選ぶ.
やがて,どの辺に沿って移っても最適解から遠ざかる特別な頂点に到達する.その頂点が最適解である.
問題を一般化して$${n}$$次元の問題(制約条件$${m}$$)を考えると,
$${m×n}$$次の行列$${A_{mn } }$$を用いて,$${z=A_{mn}x-b}$$と置くと,
$${A_{mn}x-z=b}$$なので,条件式は$${A_{mn}x-z≦b}$$,すなわち
$${\left[ \begin{array}{@{\,} cc @{\, } }
A & -I
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x \\[0mm]
z
\end{array} \right] \leqq b}$$
$${\left[ \begin{array}{@{\,} cc @{\, } }
A & -I
\end{array} \right]}$$ は2つの行列を横に並べただけの行列で,$${m×(m+n)}$$次元の行列であり,
$${\left[ \begin{array}{@{\,} c @{\, } }
x \\[0mm]
z
\end{array} \right] }$$は,ベクトル$${x, z}$$を並べただけの$${m+n}$$次元の新しいベクトルである.もちろん$${b}$$は$${m}$$次元のベクトルである.
$$ \left( \begin{array}{@{\,} cc @{\, } } 1 & 2 \\[0mm] 1 & 1 \\[0mm] 3 & 1 \end{array} \right) \left( \begin{array}{@{\,} c @{\, } } x \\[0mm] y \end{array} \right) \leqq \left( \begin{array}{@{\,} c @{\, } } 4 \\[0mm] 8 \\[0mm] 18 \end{array} \right) $$
$$\left[ \begin{array}{@{\,} ccccc @{\, } }
1 & 2 & -1 & 0 & 0 \\[0mm]
1 & 1 & 0 & -1 & 0 \\[0mm]
3 & 1 & 0 & 0 & -1
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
z_{1} \\[0mm]
z_{2} \\[0mm]
z_{3}
\end{array} \right] \le \left[ \begin{array}{@{\,} c @{\, } }
4 \\[0mm]
8 \\[0mm]
18
\end{array} \right] $$