色々な種類の楽器(弦楽器、管楽器など)は,数学の観点からは,すべて,音源が弦の振動というモデルで表すことができます.
古代では,モノコード(単一弦)が,科学的な装置としてだけでな,楽器としても機能しました.モノコードは木製の共鳴器で,その上に弦が張られ、2点で固定されています.弦の発音部分の長さは,スライド式スタンドによって可変です.
弦の特性(材質、張力)が変化しなければ,振動数$${f}$$は弦の長さ$${l}$$に反比例します:$${ f ∼ 1/l}$$
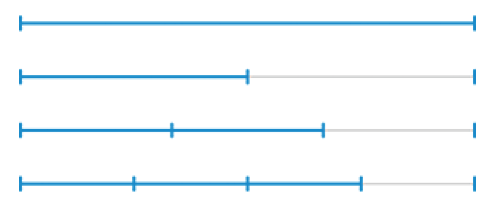
例えば,同じモノコードを2つ用意し,片方を基準とし,もう片方のモノコードで,弦の発音部分の長さを変え,色々な音程[2音の差]作ったとします.
純正律には,ユニゾン[弦長比1],オクターブ[弦長比1/2],クイント[弦長比2/3],クオーター[弦長比3/4](ユーフォニー*の高い順に並べた)があります.*[ユーフォニーとは調和の良さのこと]
弦の周波数は弦長に反比例するので,それぞれの基本音の周波数は,オクターブで2倍,クイントでは3/2倍,クオーターでは4/3倍異なります.
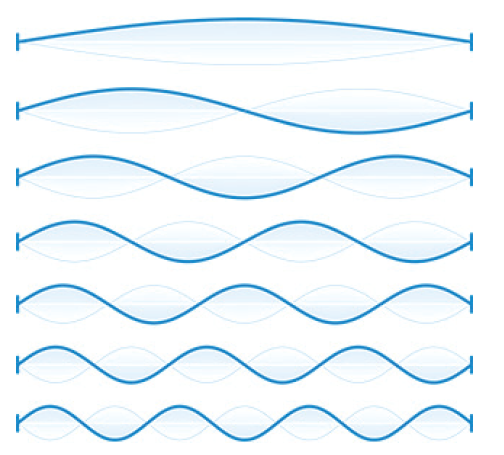
■現実に起こる弦の振動は基本周波数のみではありません.同時にいろいろな倍音が発生します.両端が固定された弦の振動は,基本音とこれらの倍音の重ね合わせになります.弦の両端の他に,$${n}$$個の節のある定在波は弦を$${n+1}$$等分するので,基音の周波数を$${f}$$とすると,倍音の周波数は$${(n+1)f}$$になります.従って,弦の周波数の完全集合は$$ \{f, 2f, 3f, 4f, …. \}$$です.
■弦楽器の音色は,周波数の集合だけでなく,種々の倍音の音量比も関係します.一般に,倍音の音量は主音より小さく,倍音の次数が増加するにつれて減少します.また,主音と倍音の調和も関係し,倍音の次数が小さい方が良く調和します.
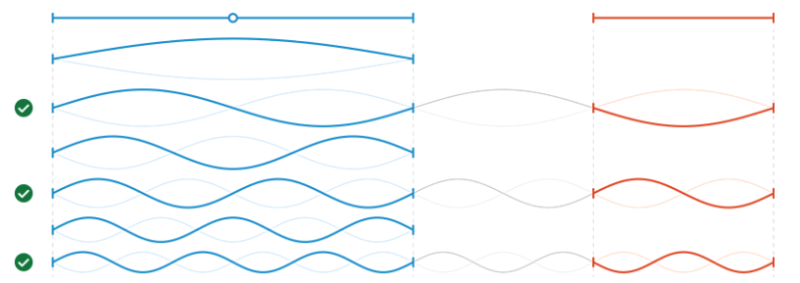
オクターブだけ異なる2つの弦は,弦長が2倍異なり,長い方の弦の周波数集合を$$ \{ f , 2 f , 3 f , 4 f , ... \} $$とすると,オクターブ高い弦の周波数集合は$$ \{ 2 f , 4 f , 6 f , 8 f , ...\} $$となります.
2番目の集合は1番目の集合の部分集合なので,オクターブ異なる2音は,似た音として知覚されるのはもっともなことです.
2つの楽器が同一音を発するユニゾンとは異なり,オクターブ異なる場合は音量(振幅)に違いができます.
オクターブでは,音量(振幅)は,長い方の弦の「偶数」の倍音に対してのみ変化し,その主音$$ \{ f \} $$あるいは「奇数」の倍音$${ \{3f , 5f, 7f,...\} }$$については変わりません.
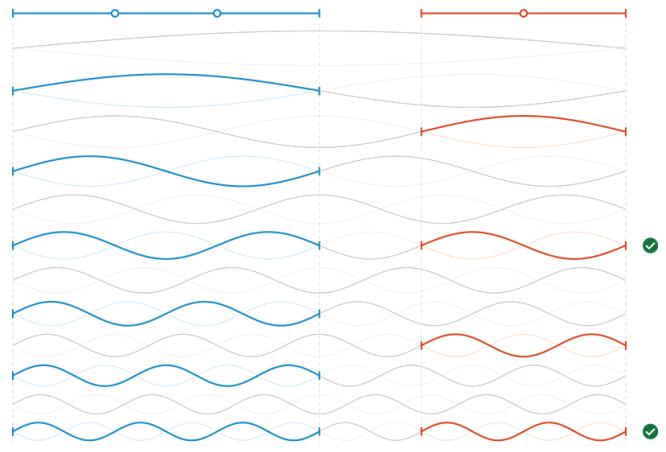
クイントを考察しましょう.クイントとは弦長の比が2/3になった場合ですから,純正律の完全5度の和音です.
$$\{f , 2f, 3f, 4f, ...\}$$が長さ$${l}$$の弦の周波数集合とすると,長さ$${2l/3}$$の周波数集合は,$$ \{ \frac{3}{2}f, 2 \frac{3}{2}f, 3 \frac{3}{2}f, 4 \frac{3}{2}f, …. \}$$となります.
短い弦の基本音$$\{ \frac{3}{2}f \}$$は,長い弦の倍音中にはないことがわかり,オクターブのユーフォニーの説明にクイントは当てはまりません.
しかし,音の知覚には,まず基本音の比較があるので,もし,長さ$${2l}$$の架空の「統一」弦を考えると,その周波数集合$$ \{ \frac{f}{2}, 2\frac{f}{2}, 3\frac{f}{2}, …. \}$$の中に,弦$${l}$$と弦$${\frac{2}{3}l}$$の基本音,および,それらのすべての倍音が現れることがわかります.
重要なのは,架空の「統一」弦の長さが$${2l}$$であることです.
この$${2l}$$という長さは,長さ$${l}$$とクイント弦の長さ$${\frac{2}{3}l}$$の最小公倍数です.
統一弦の倍音の調和のとれた世界に,両方のクイント弦の周波数を取り入れることで,聴き手は音の良さとまとまりを感じます.
クイント弦の周波数を直接比較することもできます:
弦長$${l}$$に対しての周波数集合$$\{f, 2f, 3f, 4f, ...\} $$,弦長$$\{\frac{2}{3}l\}$$に対しての周波数集合$$\{\frac{3}{2}f, 2\frac{3}{2}f, 3\frac{3}{2}f, ...\} $$でありました.
短弦のすべての「偶数」倍音は,長弦の倍音ですが,短弦のすべての "奇数 "倍音は長弦の倍音ではありません.
これらの短弦の「奇数」の倍音が,ハーモニーが不完全である理由です.クイントは調和しているが、調和の程度はオクターブより劣っているのです.
クオータの和音(完全4度)も同じように分析されます.
弦の長さが$${l}$$と$${\frac{3}{4}l}$$の場合,統一弦の長さは$${3l}$$になります.その結果,クオーターは純正律になりますが,クイントよりも調和がとれた音にはなりません.
弦の音を基本音と倍音の合成音として数学的に表現するということは,周期関数を倍音の$${sin(nx)}$$, $${cos(nx)}$$の和で表すことを意味します[長さ$${l}$$で両端固定の弦の振動はFourier級数で $${\sum_{n}^{} a_{n}sin(2n\pi x/l)}$$].
この和は,構成倍音とは大きく異なることがあります.シンプルなトーンが,豊かで表現力豊かな音色を構成します.
応用:音楽
数学: 比例、和声分析
『数学構成要素』p.98-101のテーマより.
ただし,説明は全面的に変更しました.
[追記]
私の手元には「楽器の音響学」安藤由典があります。例えばバイオリンなら弦の振動が源ですが,実際に楽器から聞こえる音は,共鳴体の胴の振動で,楽器の良し悪しは胴の特性で決まります。共鳴周波数の間隔が完全5度に近いと良いような説があります。バイオリン4弦の開放弦音のスペクトルでもそれぞれの弦で倍音の出方は異なります。G線では倍音次数とともに始めは増加が見られます。