これまでは連続体の自由度であったがこれは本質的なことではない.同様なQECCsを離散システム(スピン鎖)上で構築する.2DのPTsと同様な1Dの"フィボナッチ準結晶"を用いる.
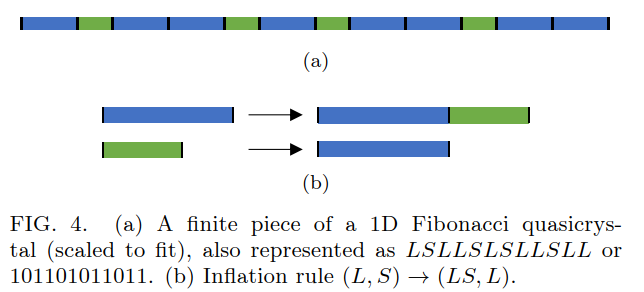
Fig.4.
■ 1次元フィボナッチ準結晶
長さL(長い)とS(短い)の2種類の区間で構成されるテッセレーションRを考える.
長さの比L/Sは黄金比: L/S =(√5+1)/2
このタイリングのインフレーションルールは (L,S)→(LS,L) (7)
図4(b) 参照
●隣接するSSやLLLなどは生じない.
[訳注1)証明]
Sが生れる原因はL(L→LS)にあるが,Sが生れるときはLSの形でLとSが同時にペアで生れる.従って,Sの間に必ずLが挟まれ,SSの型は生じない.
LLの型はあり得るが,これを生じる原因はSL(SL→LLS)のみである.LLLSを得るにはその原因がSSLである必要があるが,SSとなることはあり得ないので,結局,LLLの型は生じない.
●PenroseタイリングとFibonacci準結晶は密接な関係がある:PTのAmmann線は,5つの平行な部分集合(それぞれは正5角形の辺に平行)に分けられ,これらの平行部分集合のそれぞれは,1DのFibonacci準結晶を作る.
[訳注2)]Lの個数/Sの個数=黄金比1.618・・・・(n→∞)を証明せよ:
結局,$${\begin{pmatrix} 1 & 1\\ 1 & 0\\ \end{pmatrix}^{n}=\begin{pmatrix} a_{11} & a_{12}\\ a_{21} & a_{22}\\ \end{pmatrix} }$$ を計算することになるが,行列の各項$${a_{11}(n), a_{12}(n), a_{21}(n), a_{22}(n)}$$は,フィボナッチ数列になり,$${a_{11 } }$$に対して,$${a_{12 } }$$および$${a_{21 } }$$は1項遅れ,$${a_{22 } }$$は2項遅れである.今必要なLの数/Sの数の比は,$${a_{11}/a_{21 } }$$であり,この比は$${n→\infty}$$で黄金比1.618・・・である.
■記号置換による離散QECC
フィボナッチ準結晶の構造は,ある種の離散系にも現れる.正確には,Fibonacci準結晶を,Lを数字の1,Sを数字の0に置き換えることで,辺の無限ビット列として表すことができる.インフ
レーション・ルールは次のようになる:
(1, 0) → (10, 1) (8)
離散システムにおけるインフレーション・ルールは通常,記号的置換と呼ばれる.
ビット列のレベルでは,我々のQECCの構造を可能にする重要な性質がまだある.
全域的に不等価な(すなわち,変換によって関連づけられない)局所的には識別できない回復可能なビット列$${\{F\} }$$はまだ無限に存在する:
● Fの任意の有限部分文字列は,他の任意の文字列F′にも現れ、異なる有限部分文字列の相対頻度も一致する.(付録C参照);
● 有限領域$${K}$$内のFの任意の有限部分文字列は,Fの残りから復元できる.Fの任意の有限部分文字列(有限領域$${K}$$内)は,Fが特異な場合を除き,Fの残部(補空間領域$${K^c}$$内)から復元できる.(付録B 3参照).
したがって,これらのビット列を利用して,式(4)に類似した離散多体波動関数を構成することができる.これらの波動関数は,同じQECCに対する基底をなす.式(4)に従い,ビット文字列$${[F]}$$の各同値類に対して次のような波動関数が作れる:
$${ |Ψ_{[F]}⟩ ∝ \Sigma_{x=-\infty}^{\infty} |x+F⟩ }$$ (9)
ここで,$${x+F}$$は$${F}$$の$${x}$$だけの並進である.
これは 整数格子上の量子スピン鎖の波動関数と考えることができる.これらの量子状態$${\{|Ψ_{[F]}⟩\} }$$は,QECCのコード部分空間$${C}$$を張る.
付録Fで,これらの符号状態のエンタングルメント・エントロピーを計算する.