「アルゴリズム」という言葉は,ペルシャの偉大な科学者アル=フワリズミの名前に由来する.アル=フワリズミは,9世紀に数位システム[10進法数表記]を記述した(代数学という言葉も同じ著作に由来する).
イスラム黄金時代の数学(9 世紀から 10 世紀)は,ギリシャ数学 (ユークリッド,アルキメデス,アポロニウス) とインド数学 (アリヤバータ,ブラフマグプタ) の上に発展し,分数を含む完全な小数位システムの開発,代数学の最初の体系的な研究,幾何学と三角法の進歩など,重要な進歩があった(10~12世紀).
https://academic-accelerator.com/encyclopedia/jp/mathematics-in-the-medieval-islamic-world 参照◆
整数や有理数を演算するアルゴリズムは,数値アルゴリズムと呼ばれる.
アルゴリズムの対象は一般化されて,グラフ,配列,テキスト,スケジュールなど任意の離散データ(グラフ,配列)を扱うものにも及ぶ.
これらは,K.ゲーデル,А. A.マルコフ,P.S.ノヴィコフ,A.チューリング,A.チャーチといった前世紀の偉大な数理論理学者の著作で定義され,計算できる厳密な理論が作られた.
Математическая составляющая, p.262-275参照◆
アルゴリズムは,広義には,完全に定義されたルールの集合で,有限時間でゴールに到達できる手順を定めるものである.
一つの問題を解く手順にも異なる色々なアルゴリズムがある.また,ある問題に対する同じアルゴリズムであっても,問題 に与えられた数値に応じて効力が変わる.アルゴリズムの質を数値化することは容易ではない.
アルゴリズムの「質」を,ある「複雑さ関数」によって測定することが,この複雑さ理論の目標である.
あるアルゴリズムでの試行回数を測定してみると,特定のある入力値の場合には偶然にも1回で答えが出たりする.2つの異なるアルゴリズムを比較した場合,与えられた特定の入力値に対して試行回数が逆転することもある.このようにアルゴリズムの複雑さの尺度を決めるのは非常に困難な問題である.アルゴリズムの複雑さは,最悪のケースを評価の対象として決める.
その複雑さを数値で完全に定義することは難しい.
このため,普遍的尺度は,古典的な計算理論の枠組みの中で,次のレベルの一般化としてのみ導入できる.これは,チューリング・マシンのクロック・サイクル数と呼ばれる.チューリング マシンは,1936 年に英国の偉大な数学者 A. チューリングによって提案された抽象的なコンピューティング デバイスで,直感的には,これは目標を達成するために必要な基本的 (分解不可能な) ステップ数である. プログラムの動作期間全体にわたって,プログラムに含まれる命令の実行数をカウントすることと理解することもできる.これは実行の数であり,命令の数とは異なる.後者はいわゆるコルモゴロフ複雑性であるが,ここでは考慮の対象としない.
これを説明するために,2つの整数(例えば,630と300)の最大公約数gcdを求める例を考察する:
(方法1)最大公約数は$${2・3・5=30}$$である.
(方法2)それぞれの数を素因数分解する.
$${630=2・3^2・5・7}$$
$${300=2^2・3・5^2}$$
これから,最大公約数$${2・3・5=30}$$が得られる.
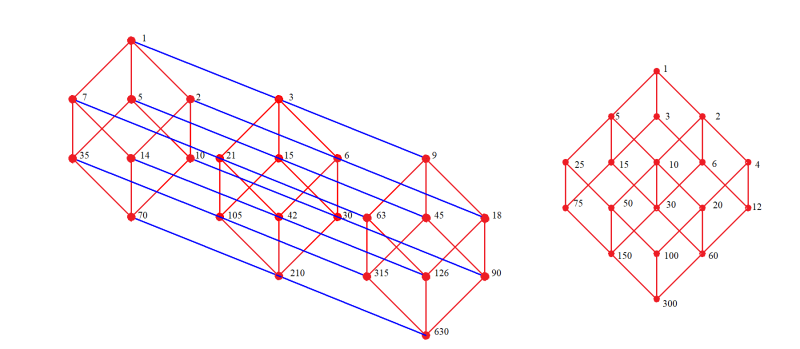
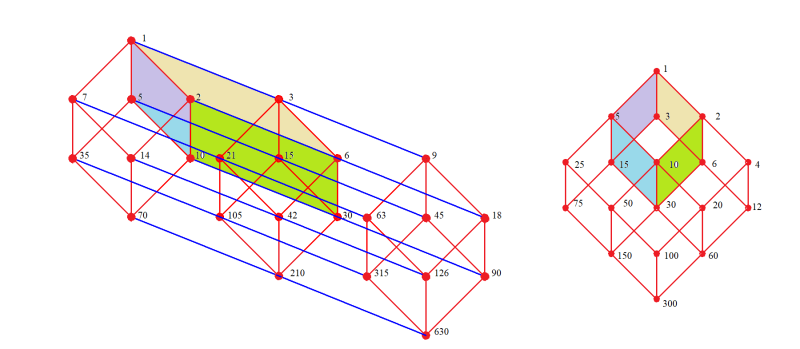
それぞれの数の約数構造を整理するのに,亀井図(多元構造図)は有用である.
両方の数に含まれる互いに素な辺$${2,3,5}$$で生成される平行6面体の頂点が共通な約数を与える.最大公約数は30.
亀井図による630と300の約数構造の表現
630と300公約数部分のグラフ
(方法3)ユークリッドのアルゴリズム(互除法)を使う.
630=2・300+30
300=10・30+0
従って,最大公約数は30である.
(注)ユークリッドのアルゴリズム
$${a<b}$$のペア$${(a,b)}$$に対して,$${b}$$を$${a}$$で割って余りを出す: $${b =h・a +r}$$ここで$${0≦r≦a-1}$$.次に,このアルゴリズムをペア$${(r, a)}$$に再帰的に適用する: $${a}$$を$${r}$$で割り,$${a =u・r +s}$$となり,再帰的にとは,$${(a,b)}$$を$${(r,a)}$$で置き換え手順を継続することである.これを$${(0,d)}$$の形になるまで続ける.このとき得られた$${d}$$が最大公約数である.-----------------◆
ユークリッドのアルゴリズムが正しく機能するのは,$${gcd(a, b) =gcd(r, a) =・・・=gcd(s, r) =...}$$だからである.最大公約数は,この変換手順の不変量である.従って,最後のペア$${(0, d)}$$は最大公約数$${d}$$に帰着する.
$${(a+r)≦(2/3)(a+b)}$$が常に成り立つので,組の数の和は指数関数的に減少し,このアルゴリズムは$${f (n) ≈ 10n}$$反復で収束する.
これは,$${a}$$ と$${b}$$ の表記におけるビット数 $${n}$$ の一次関数である.
関数$${10n}$$が,多項式である(指数関数ではなく,ある$${C, d>0}$$に対して$${C・n^d}$$の形をとる)という事実は重要である.
現代の複雑さ理論では,(最悪の場合の)複雑さの見積もりが多項式(速く計算できる)であるアルゴリズムのクラスは多項式( "P ")と呼ばれる.