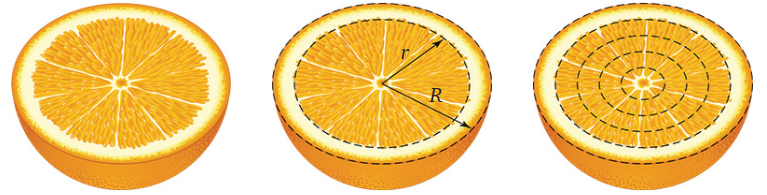
オレンジを買ってきて半分に切った.
オレンジの半分に,皮と果肉のどちらが多いか見た目で わかりますか?
この質問は奇妙に思える.なぜなら,皮はオレンジの端の薄い層なのだから.しかし,球の端にある比較的薄い皮は,他の部分と同じ体積を持つことが分かった.例えば,直径10cm,皮の厚さ1cmのオレンジの場合,全体の体積のほぼ半分が皮の体積である.調べてみよう.半径$${R}$$と$${r(r<R)}$$の2つの球を考える.
小さい方の球の体積が,大きい方の球の体積の半分になるような球の半径は?半径 $${R}$$の球の体積は$${V_{R} = 4/3 \pi R^3}$$
題意の$${r}$$を見出すには
$${V_{r}=V_{R}-V_{r } }$$ $${4/3 \pi r^3 =4/3 \pi R^3 -4/3 \pi r^3}$$
これから,$${R^3 =2r^3}$$ が得られる.すなわち,
$${r=R/ \sqrt[3]{2} \fallingdotseq0.79R\fallingdotseq4/5 R}$$
このように,球の体積の半分が,半径の1/5の表面近くの層に集中している.図のオレンジでは、果皮と果肉は等しい.
嫌な薬を飲むように子供を説得するにはどうしたらいいのだろう?
数学的なトリックがある.うまくいったら、薬に加えて、詳細説明も飲み込ませることができる.
混合薬を円錐形のグラスに注ぎ,「病人」に半分飲むように勧めると,たいていの人は「半分」を自動的に「半分の高さ」だと思い込み,グラスの中身の$${7/8}$$,つまり,ほとんど全部を飲むだろう.
実は,液面が約$${1/5}$$下がると,グラスの半分が飲み干される.
これは,オレンジの例で計算したのと同様である.
証明は,球の体積の公式ではなく,同様な円錐の体積の公式に置き換えるだけだ.これは,どのような形の円錐グラスでも成立する.
応用:日常生活
数学:円錐、円錐の体積
『数学的構成要素』p.92ー93 より抜粋