表題テーマの「数学月間懇話会(第19回)」を,2023年7月22日,13:00-17:00,東京大学数理科学研究科棟002教室にて実施しました.主催はNPO法人数学月間の会(理事長:岡本和夫)です.
以下の2つの講演(それぞれ90分)により構成され,総合司会を稲葉寿(東京学芸大)が行いました.(注)2020年の数学月間懇話会で実施した講演:感染症の数理モデル,稲葉寿(東大)も参照
(1) パンデミックで活躍する数理モデル:國谷 紀良(神戸大学大学院システム情報学研究科)
(2) 新型コロナウイルス感染症のデータサイエンスと政策科学;土谷隆(政策研究大学院大学)
今回は,講演(1)を紹介します.講演(2)は次号で紹介します.
(注)2021年の数学月間懇話会で実施した講演:新型コロナウイルス感染症と統計数理, 土谷隆(政策研究大学院大学)も参照
講演(1)國谷 紀良(神戸大学大学院システム情報学研究科)
■まず,感染症の数理モデル(集団内での感染症の流行を表す微分方程式など)の研究史の概略紹介がありました.
SIRモデルとは,集団が3つの部分集団$${S,I,R}$$で構成されるとして,それらの集団の増減を微分方程式で表したものです.ここで,$${S}$$は,感受性(感染可能性)のある集団,$${I}$$は,感染中で他人を感染させる力のある集団,$${R}$$は,回復集団(再感染はしないと仮定)です.
感染率$${\beta}$$,回復率$${\gamma}$$とすると,SIRモデルの基本微分方程式が得られます:
$${S'=-\beta SI}$$, $${I'=\beta SI-\gamma I}$$, $${R'=\gamma I}$$
これは,ケルマックとマッケンドリックが1927年に発表した論文「感染症流行の数学的理論への貢献」によります.
感受性のみの集団に侵入した1感染者が算出する新規感染者数を「基本再生産数」$${R_0}$$といい,$${R_0>1}$$のときに流行が起こります.
感染症の種類,ウイルス株,国や地域によって$${R_0}$$は独特の数値を持ち,麻疹は12-18,インフルエンザで1.2-1.4ですが,covid-19では2.4-3.4でした.
果樹園における感染症の伝搬を,格子点上の隣接する木から感染する確率を$${p}$$として,モンテカルロ法によるパーコレーションの研究をし,流行の臨界値を研究したのは,ブロードベントとハマーズリー(1957)でした.
SEIRモデルは,感受性$${S}$$の集合から感染$${I}$$の集合に移る間に,潜伏期$${E}$$の集合を入れて得られます.このとき,$${E}$$から$${I}$$への遷移確率$${\varepsilon}$$を入れます.微分方程式は次のようになります:
$${S'=-\beta SI}$$, $${E'=\beta SI-\varepsilon E}$$, $${I'=\varepsilon E-\gamma I}$$, $${R'=\gamma I}$$
SEIRモデルを日本の流行初期(2020/1/15)~2/29)のデータに適用して,基本再生産数$${R_0}$$を推計すると,$${R_{0}=2.6}$$が得られました.
■緊急事態宣言などの介入の効果検証
不要不急の外出自粛,飲食店,映画館,デパートなどの休業,テレワークの推進などが行われ,「接触8割減」が提唱されました.
第1回目緊急事態宣言(2020/4/7-5/25)では,期間中に実効再生産数が減少し,期間の最後で最小値になり,期間終了解除後にリバウンドが現れました.感染率の減少割合$${r^{*}=0.86}$$, 実効再生産数$${R_{c}=(1-r^{*})R_{0}=0.36}$$
■無症候感染を含むSEIRモデルは,次のようになります:
$${S'=-(\beta_{1}E+\beta_{2}I)S}$$, $${E'=(\beta_{1}E+\beta_{2}I)S-\varepsilon E}$$, $${I'=\varepsilon E-\gamma I}$$, $${R'=\gamma I}$$
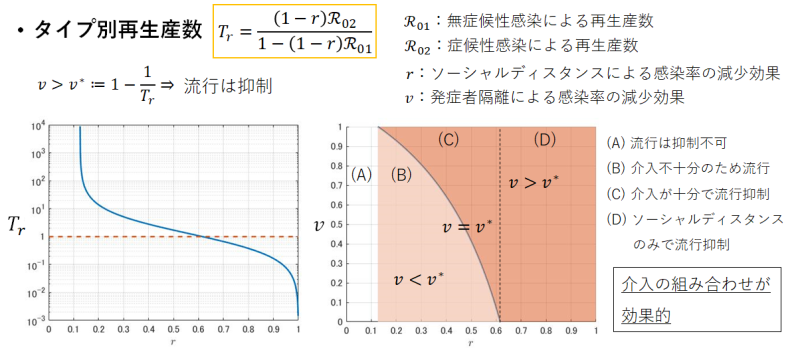
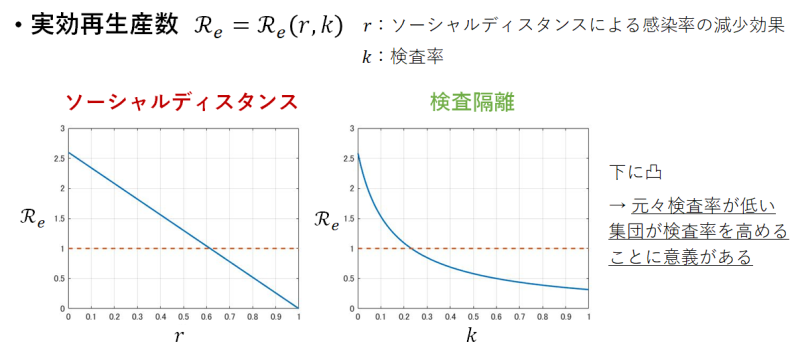
SRIRモデルを用いて,流行の抑制に十分な発症者隔離率$${\nu}$$を求めます.ソーシャルディスタンスによっても,発症者隔離によっても感染率の減少効果はみられますが,介入の組み合わせが効果的であることを示すマップ(横軸:ソーシャルディスタンスによる感染率減少効果,縦軸:発症者隔離による感染率減少効果)が得られました.
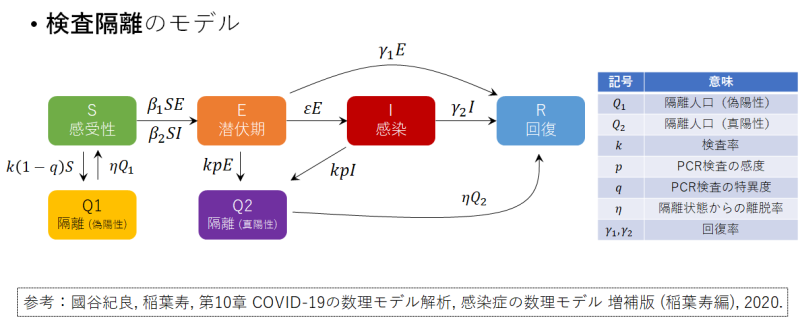
検査隔離のある状態モデルでは,偽陽性による隔離と真陽性による隔離の2つの部分集団が追加されたものです.
■数理モデルはワクチン接種法の検証にも適用した.
COVID-19に対し,累積死亡者数を最小化するためのワクチン1回目と2回目の最適な接種間隔を,構造化感染症モデルによって調べ,
ファイザーとアストラゼネカを想定したパラメータでは,いずれも接種間隔が3~4週間よりも長い方が良いという結果を得た.
感度分析では,仮想的なワクチンの2回目の意義が大きいほど,短い接種間隔が最適であるという示唆が得られた.
■研究中課題
均質ではない集団(年齢構造化など)にSIRモデルを適用したり,出生と死亡を含むSIRモデル,平衡解の大域安定性の問題,周期解の存在など興味深い問題の研究も行っている.