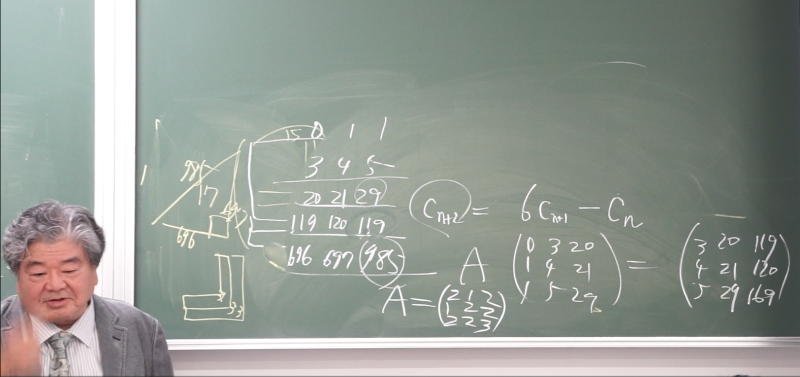2024数学月間(第20回)の第3日目(2024.08.05)は,東京大学数理科学科棟002教室で開催されました.2番目の講演[15:20-16:50]は;
「古代の数学エジプト紐と現代のピタゴラス三角形3分木」亀井喜久男(愛知県立大)でした.
講演録筆者の独断で,講演者が言及できなかった部分を補ったり,読者の理解の助けになるように筆者の解釈で図を作成したりした部分があります.もし,筆者作成の図などに,筆者の誤解による誤りがあればお詫びし修正します.(講演録文責:谷)
■ (I)エジプト紐
エジプト紐とは,輪になった紐に,時計の文字盤のように12等分の標が着いたもののことです.輪の周長は,120cm,12m,120m,60cm,6m,60mなどが使いやすいようです.実際の測地目的にあった長さのものを使います.机上の学習用には,60cmが使い良いようです.
なぜ,12等分したかと言えば12は約数が多く,エジプト紐で作れる角度の多様性が大きいからです.エジプト紐を教材として考案したのは講演者の亀井喜久男氏です.
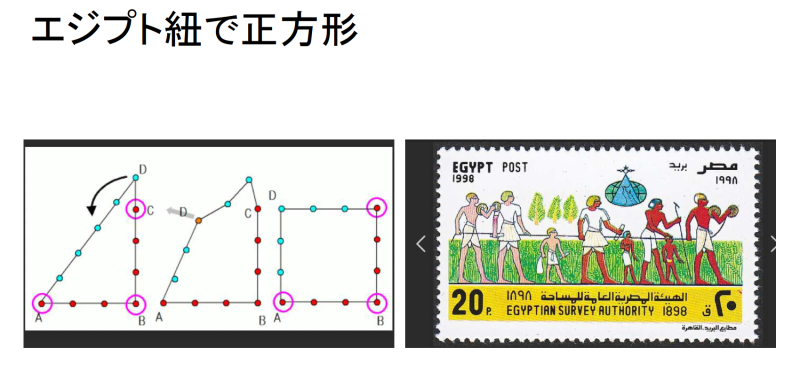
■エジプト紐の基本
エジプト紐で直角(3,4,5の直角三角形)を作るのが基本作図です.
条里制遺構の調査によれば,1町は60間(約108m)で,1辺が1町の正方形の面積は1町歩です.我が国の出雲国風土記に180間の縄の活用が見られます.これをエジプト紐として用い,一辺が60間の正方形を描くと,その面積は1町歩です.古代メソポタミアにもこの技術はあったはずで,一辺が60m(1イク)の正方形の畑を区画しその面積を測量したそうです.
このように古代から野外で実用に使われた技術を体験して理解しよう.
●グラウンドに大きな色々な図形(ハンドボールコートなど)を描く実習:
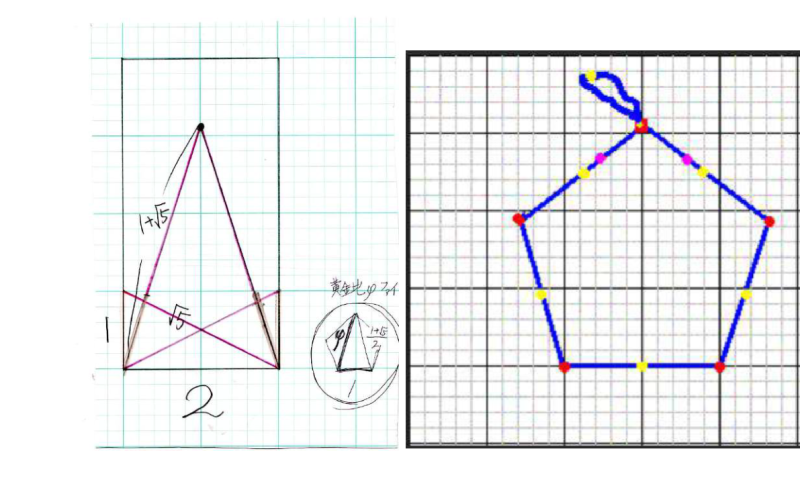
● 正5角形を描く
ちょっと工夫すれば正5角形も作れます.$${1+\sqrt{5 } }$$の長さを作るのがミソで,仕上がった正5角形は一片の長さが$${2}$$で,エジプト紐$${12}$$の長さ全部は使いません($${10}$$の長さだけ使います).
● 色々な図形を作る手順を考えることは,良い教育になります.
正6角形,6角星形,正8角形,正12角形,正9角形などはエジプト紐で作ることができます.手順を工夫してみよう.
■ (II)ピタゴラス三角形3分木
直角3角形ではピタゴラス 方程式$${a^2+b^2=c^2}$$が成立します.この整数解$${(a,b,c)}$$はピタゴラス数と呼ばれますが,$${a,b,c}$$に公約数がない(互いに素)場合$${(a,b,c)}$$を,特に,原始ピタゴラス数(primitive Pythagorean triples),その三角形を,原始ピタゴラス三角形と言います.
◆講演録著者注)R.Courant and H.Robbins『What is MAthematics?』(1941)森口繁一監訳:細矢治夫『三角形の七不思議』では,「既約ピタゴラス三角形」と呼んでいます.当NPO会員の竹内淳実により,計算された$${c<20,000}$$の既約ピタゴラス数のリスト(2015年)は,当会HPに掲載しています.
原始ピタゴラス数3つの系列
原始ピタゴラス数には,次の3つの系列があるのは公知です:
(1)ピタゴラスの系列
$${(a,b,c)}$$:$${(3,4,5),(5,12,13),(7,24,25),・・・・・}$$
$${a}$$は奇数.$${b=(a^2-1)/2}$$.$${c=b+1}$$.
斜辺は奇数.偶数辺(足)は斜辺より1だけ小さい.
(2)プラトンの系列
$${(a,b,c)}$$:$${(4,3,5),(8,15,17),(12,35,37),・・・・・}$$
$${x}$$は偶数.$${b=x^2-1}$$.$${c=x^2+1}$$.$${a=2x}$$
斜辺は奇数.奇数辺(足)は斜辺より2だけ小さい.
(3)フェルマーの系列
$${(a,b,c)}$$:$${(3,4,5),(20,21,29),(119,120,169),(696,697,958),・・・・・}$$
斜辺は奇数.直角を挟む2辺(足)の差が1.
[亀井の研究]
フェルマーの系列に対する漸化式の発見(亀井,1991).
$${a_{n+2}=6a_{n+1}-a_{n}+2}$$
$${b_{n+2}=6b_{n+1}-b_{n}-2}$$
$${c_{n+2}=6c_{n+1}-c_{n } }$$
これからフェルマーの系列の原始ピタゴラス三角形に作用させ次の原始ピタゴラス三角形を生む演算子$${A}$$を導きました.$$ A=\begin{pmatrix} 2&1&2\\ 1&2&2\\ 2&2&3\\ \end{pmatrix} $$
つまり,$${\begin{pmatrix} 2&1&2\\ 1&2&2\\ 2&2&3\\ \end{pmatrix}\begin{pmatrix} 3\\ 4\\ 5\\ \end{pmatrix}=\begin{pmatrix} 20\\ 21\\ 29\\ \end{pmatrix} }$$などです.同様にして,
ピタゴラス系列を生む演算子$$ \begin{pmatrix}1&-2&2\\ 2&-1&2\\ 2&-2&3\\ \end{pmatrix} $$
プラトン系列を生む演算子$${\begin{pmatrix}-1&2&2\\ -2&1&2\\ -2&2&3\\ \end{pmatrix} }$$ も求めました.
独自で行ったこの証明を整数論の先生に提出しましたが,残念なことに先行研究がアメリカにあったようです.
[亀井喜久男『Focus Gold通信vol.6,p.11-13,』]
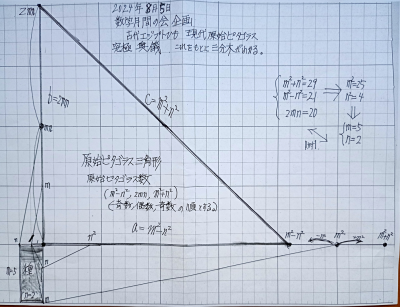
原始ピタゴラス数の3分木構造
ピタゴラスの定理$${a^{2}+b^{2}=c^{2 } }$$を満たす互いに素な正整数の3組数$${(a,b,c)}$$を求めると,$${a=m^{2}-n^{2}, b=2mn, c=m^{2}+n^{2 } }$$, ($${m,n}$$は正の整数)を得る.$${c}$$は斜辺,$${a, b}$$は直角を挟む2辺であり足と呼ぶ.結局,偶奇性のことなる2つの正の整数$${m>n>0}$$により全ての原始ピタゴラス数は網羅される[ピタゴラスの公式と呼ばれる].これは,ピタゴラスより1500年も古いバビロニア時代から知られていたという.[Neugebauer:The Exact Sciences in Antiquity(1961), ChapII, Babylonian Mathematics]
原始ピタゴラスの3つ組数$${(a,b,c)}$$と$${[m,n]}$$とは1:1対応をする.$${[m,n]}$$のことを亀井は種,$${(a,b,c)}$$を実と呼んでいる.
◆講演録著者注)----------------------
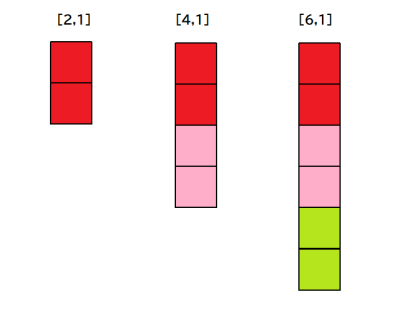
原始(既約)ピタゴラス三角形を,$${m,n}$$平面上にプロットした原始ピタゴラス三角形の分類[細矢治夫;三角形の七不思議(2013)]類は,斜辺$${c}$$から偶数足$${b=2mn}$$を減じた$$ c-b=(m^{2}+n^{2})-2mn=(m-n)^{2 } $$は,$${m,n}$$は偶奇性が異なるので,奇数の2乗であることに注目し,
斜辺と偶数足の差の値で分類するL系列と,斜辺と奇数足の差$${c-a=2n^2}$$の値で分類するM系列での分類で,ここで考察しているピタゴラス系列,プラトン系列,フェルマー系列の分類とは観点が異なります.
---------------------------------------------
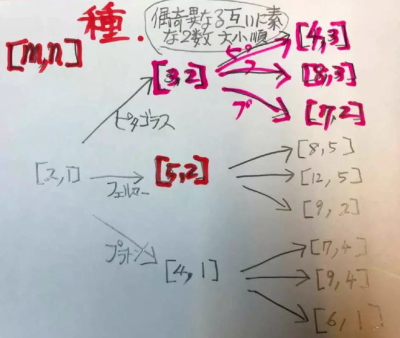
もちろん,原始ピタゴラス数に3分木構造があれば,これらと1:1の対応のある原始ピタゴラス数の種においても 分木構造があるはずです.
原始ピタゴラス数の種となる2数[$${m,n}$$]の3分木
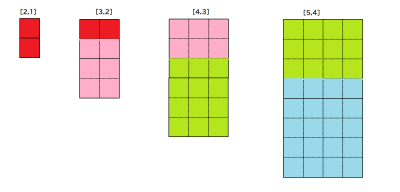
種に関する3分木構造を考えたときに,それら種間の推移演算子がどのようになるのか,講演録筆者は知りません.種間の推移演算の図形的な解釈が,亀井喜久男,島田正雄により議論されましたが,読者にとってもこれは理解しにくいと思いますので,私の理解できた範囲で,具体的な原理図(図a~c)を作成してみました.私は,これらの図形変形が推移演算と等価であることの確認をしたわけではありません.
フェルマー系列の種図形の推移は,互除法の図形解釈のようでもあり,フラクタル構造が隠れているようでもあり興味深いものです.
図a フェルマー系列の種の推移
図b プラトン系列の種の推移
図c ピタゴラス系列の種の推移
■ 種[$${m,n}$$]から三角形$${(a,b,c)}$$への作図による復元方法について,亀井による図解説明($${[5,2]}$$の例)がありました.