━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2023.03.14] No.465
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
先週は、京都大学の教育数学研究集会3/6-9に参加しました.そこで,ChatGPTとDuolingoの話がでました.
皆様はご存じだったかもしれませんが、私はこれらを知りませんでした.
ウエブで探して使ってみるとどちらも非常に面白い.
ChatGPTとは対話型のAI,Duolingoはゲーム感覚で英語の学習ができます.
さて,今回のメルマガで取り上げるのは,デュードニーのタイル張りパズルです.これは;
正3角形を多角形に分割してそれらの全部品を組み合わせて正方形が作れます.このようなことのできる最小の分割数はいくつですか?
この問題は、1905 年 2 月 1 日と 8 日の問題で Henry Dudeney によって Daily Mail の読者に提示されました。
寄せられた何百もの回答の中で、正解は 1 つだけでした。4 つの部分で十分です。
https://etudes.ru/models/dudeney-dissection/
上記のリンクにあるアニメーションを見ると正解がわかります.しかし,この解の仕組みを見つけるのはなかなか難しいので,解説用の図を以下に2つ作りました.重ねた図形の2回回転対称性に注目すれば,非常に簡単に解けます.
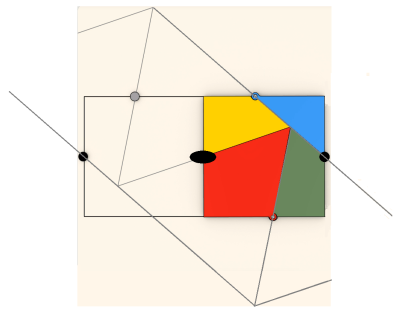
Fig.1 正方形と正3角形は同一の面積です.2つ並んだ正方形と2つ並べた正3角形を,それぞれの中点の上で重ね合わせます.この点は2回回転対称軸があります.これだけでは,重ね方にまだ任意性がありますから,正3角形を連ねて作った帯の上側の辺,下側の辺が,それぞれ,2つ並べた正方形の右側の正方形の右側の縦の辺の中点,および,左側の正方形の左側の縦の辺の中点を通過するようにします.これらの条件は同時に満たされることは,2回回転対称性から明らかです.
Fig.1
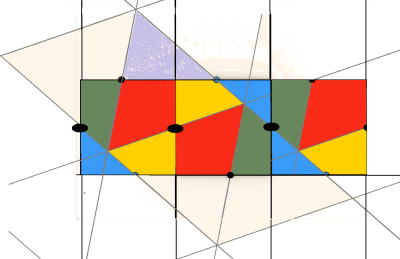
Fig.2
Fig.2を見ると,正方形の中は、赤,黄,緑,青のパーツで構成されることがわかります.一方,正3角形は,赤,黄,グレーのパーツで構成され,正3角形と正方形は面積が等しいから,部品の面積について,グレー=緑+青 の等式が成立します.従って,正3角形も赤,黄,緑,青のパーツで構成できることがわかります.