正則点系
点の多重度とその相対数の積の保存則
[訳者注)単位胞中に存在する原子の数によっては,対称性(多重度)によりその原子の存在できる場所が決まっつているという便利な性質が,構造解析のときに利用できる]
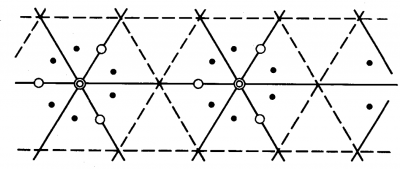
有限図形の点系(同価な点の系)に関して,対称(正則)の概念には,すでに出会っています.この概念を無限の平面図形に拡張するのは困難ではありません.何らかの無限の平面図形(下図173)が与えられたとしましょう.その中の任意の1点(図173の任意の●)を選び,選んだ点に同価なすべての点を見出しましょう.
[訳者注)同価な点というのは,対称操作で互いに変換できる点のことで,図173の場合には,実線が鏡映面,および,各鏡映面に沿った並進が定義されています]
その結果得たすべての点の集合は,同価点の1つの単純正則点系を作ります.これに,2番目,3番目,等々の同価点系(○,◎)を加えると,複雑,あるいは,複合点系を得ます.もし,単純点系の初めの点が対称面上や対称軸上や,対称中心になければ,得られた集合は一般点の同価点系(●)と呼ばれ,他の場合は,特殊点の同価点系(○,◎)と呼ばれます.
[訳者注)●だけ集めると一般点の系,〇だけ集めたものは鏡映面上の特殊点の系,◎だけ集めると鏡映面の3重点(あるいは,3回軸)上の特殊点の系]
無限パターンの各タイプ点系の点の数は無限ですが,単位胞の中の点の数は有限です.(これらは対称演算により互いに移り合う)
図173を調べると,◎の点1つに〇の点3つ,●の点6が対応し存在することがわかります.これを,●の多重度は1,○の多重度は2,◎の多重度は6であるといいます.黒点●の位置を徐々に対称面方向に動かすと,それが対称面上を通過するとき,両側から近づいた2つの黒点●は1つに合体します.もし,黒点●が3回転軸の位置に近づき,ちょうど軸上(に3つの対称面の交差点)を通過するときには,6つの黒点が1つに合体します.
したがって,各単位胞の中にある,さまざまなタイプの点の相対数$$n_{i}$$は,対応する多重度$$s_{i}$$の逆数に比例することになります.
$$n_{1}:n_{2}:n_{3}: \cdot \cdot \cdot \cdot \cdot =\displaystyle \frac{1}{s_{1 } }:\displaystyle \frac{1}{s_{2 } }:\displaystyle \frac{1}{s_{3 } }: \cdot \cdot \cdot \cdot \cdot \cdot $$
$$n:n_{1}:n_{2}: \cdot \cdot \cdot \cdot \cdot =1:\displaystyle \frac{1}{s_{1 } }:\displaystyle \frac{1}{s_{2 } }: \cdot \cdot \cdot \cdot \cdot \cdot ,$$ あるいは,$$n=n_{i} \cdot s_{i}$$
どんなパターンにも多重度s=1の点が存在するので,そのような点の相対数をnと記すと2番目の式のように書き換えられます.
言い換えると,特定の種類の点の相対数とその多重度の積は一定です. したがって,図173のパターンの例では,点の多重度と相対数の積は常に6に等しくなります. 黒点●の場合は1x 6,白点〇の場合は2 x 3,二重円◎の場合は6 x1です.
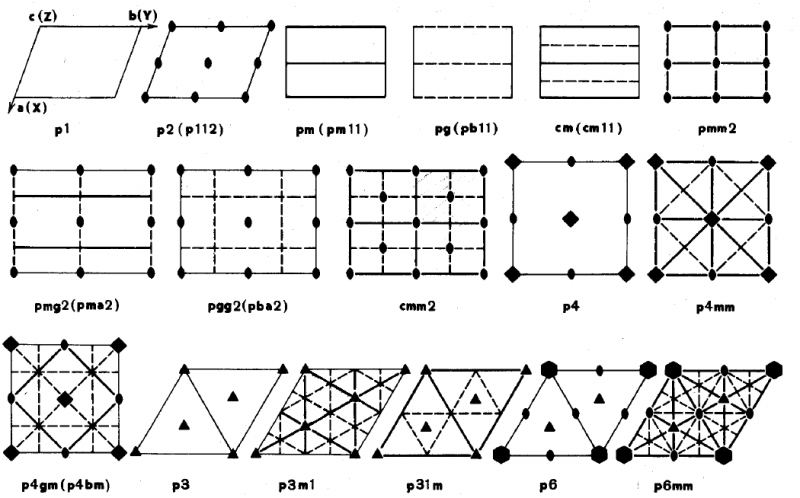
規則的な点の系(正則点系)を記述するのに,平面パターン全体を作る必要はありません. 対称要素の集合をその特定の領域(たとえば単位胞の内)で指定するだけで十分です. 対称要素の配置図が与えられれば,特定の位置に点を配置し,その対称要素を作用させて,与えられた対称クラスに対応する同価点の系を簡単に構築できます.
[訳者注)下図の2つは,対称要素の配置図(上図)に対して,一般点に非対称図形楔型を置いて得た点系(下図)の例です]