万華鏡でネットワークパターン

万華鏡でネットワークパターン
 
［訳者注］ここでは万華鏡で作るネットワークパターンについて述べているが，平面のタイル張りの対称性（5つのブラベー格子）が念頭にある．万華鏡は鏡の組み合わせで作られる対称性なので，そのうちの4つのブラベ格子が実現しうる．これらは格子の対称性そのもの（その格子で許される最も高い対称性）で完面像と呼ばれる．

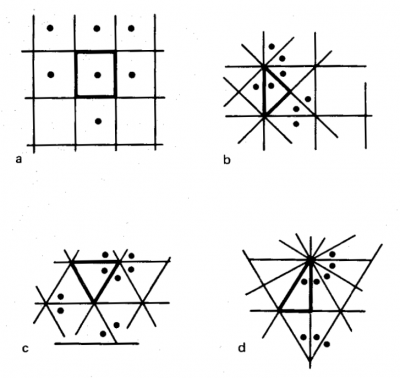
完面像クラスの４つのパターンだけが万華鏡で作ることができる．これらは紙の折り畳みとカットにより作れるパターンと同一である．長方形の辺に沿って鏡の表面が内部に向くようなプリズム配置からは，(b:a):2･m型のパターン（図170a）が生れる．元の物体はプリズムの内部に置かれる．直角2等辺3角形の周りに置かれた鏡配置により(a:a):4･m型のパターン（図170b）が生まれる．正3角形の辺に沿って配置された鏡の万華鏡は(a/a):m･3型のパターン（図170c）を生む．そして，鋭角が30°, 60°の直角3角形の辺に沿って3枚の鏡を配置した万華鏡は(a/a):m･6型のパターン（図170d）を生む．実際には，これらの万華鏡は，帯状の鏡を繋ぎ合わせて作る．プリズムの底を艶消しガラス，もしくは，外部あるいは内部に艶消しガラスの物体を置く．初めの２つの場合は，万華鏡を水平に持ち，光源に直接向ける．最後の場合は，垂直に持ち下から照明する．

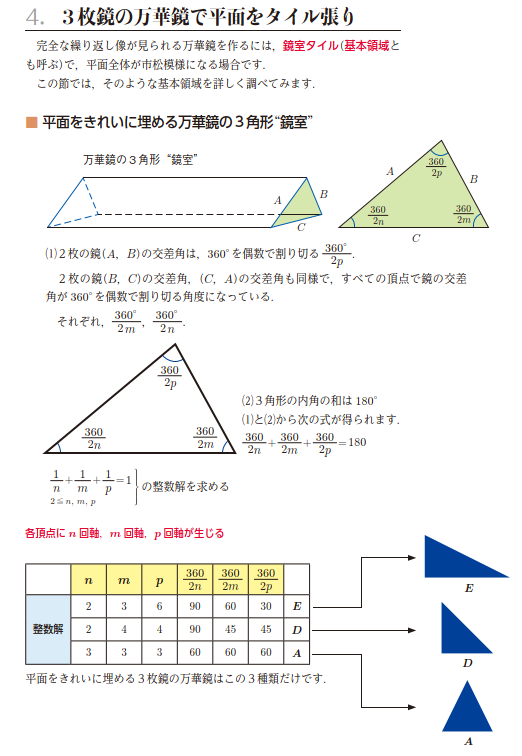
［訳者注］ここで実現される万華鏡は，4枚鏡の長方形の他に，平面を隙間なく埋め尽くす３角形の3種類（以下の説明では整数解の3角形）に関するものだけで，分数解の3角形は考慮していないので，以下の説明を補足したい：

美しい幾何学，p109，p118より