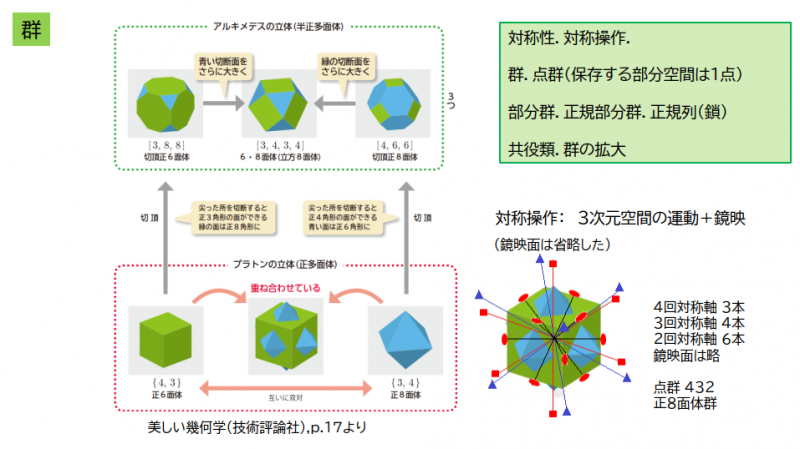
◆互いに双対な図形の対称性は同一.
◆鏡映操作と回転操作の違い:
3次元空間の物体とその鏡映像(互いにキラル)は,3次元空間内の運動で物体に重ねることができない.ただし,次元を1つ上げた4次元空間ならばこれは可能である.
◆[必要な群概念]群,部分群,正規部分群,正規列,共役類,群の拡大.
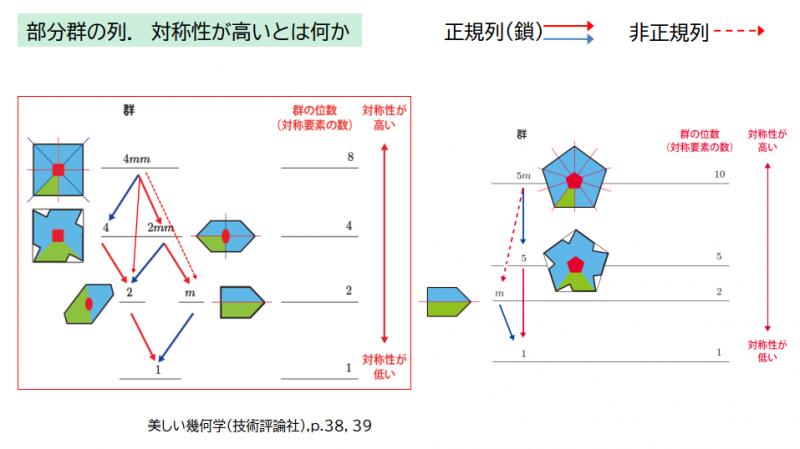
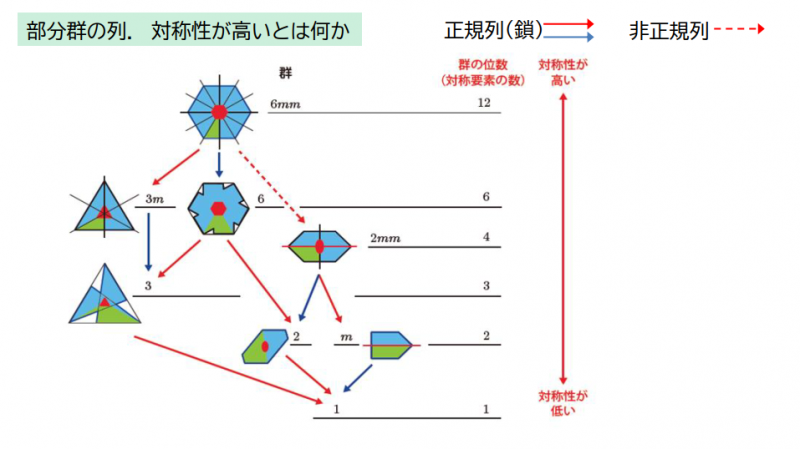
◆対称性の高低とは何かを,部分群の列(正規列,非正規列)で説明する.
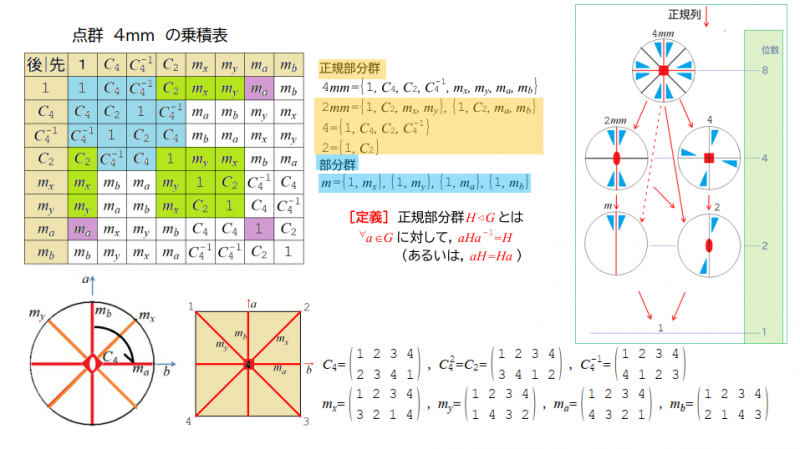
[群概念の演習]群の乗積表.点群$$4mm$$の中の部分群と正規部分群を見いだせ.
正規部分群 ; $$2mm$$, 4, 2. 部分群;$$m$$.
正規部分群$$H⊲G$$の定義は,任意の$$a∈G$$に対して$$aHa^{-1}=H$$となることである.
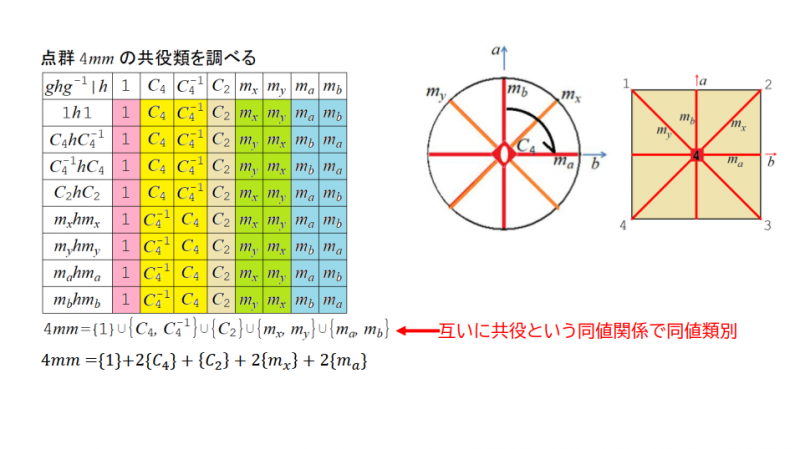
正規部分群であるかのチェックは,「点群$$4mm$$の共役類を調べる」を参照せよ.
互いに共役という関係は同値関係である.効果が同等な対称操作は同じ共役類に属することがわかる.表中に点群$$4mm$$の共役類を色分けし表示した.
◆群の行列表現には,ここでは深入りしない.異値の既約表現の数は共役類の数だけある.
例えば,シクロブタジエン(点群$$4mm$$)のπ電子系の分子軌道(4つのC原子の原子軌道の線形結合)の永年方程式(固有値問題)を解き,エネルギー準位などが求まる.あるいは,4つの原子軌道関数を基底にして作った分子軌道(点群$$4mm$$)の正則表現を簡約して,それに含まれる既約表現を求めるのだが,各既約表現はエネルギー準位に対応する.
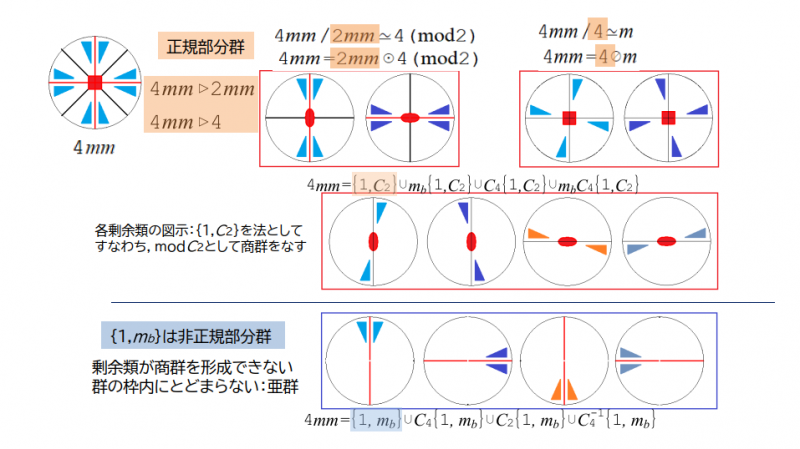
点群$$4mm$$には,$$2mm$$あるいは4が正規部分群として含まれる.点群$$4mm$$の正規部分群を核として準同型写像すると,点群$$4mm$$は商群に還元できる:$$4mm/2mm=4$$(mod2), $$4mm/4≅m$$.
部分群$$C_{2}$$あるいは$$m$$は,$$4mm$$の正規部分群ではないので,ラグランジュ展開はできるが,剰余類は群をなさない.
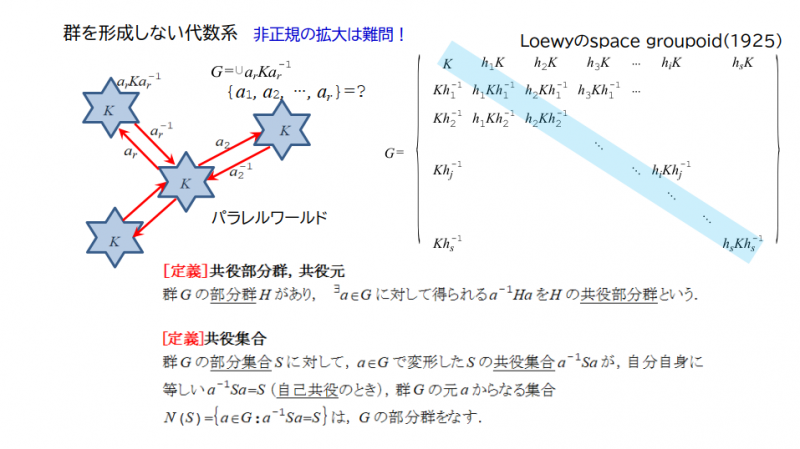
大きな群は,その正規部分群を,何らかの部分群(あるいは正規部分群)で拡大した構造になっている.これを正規拡大という.非正規の部分群を,何らかの非正規部分群で拡大した構造は,非正規の拡大という.非正規拡大は難問.例えば,部分群$$K$$の共役集合の重畳という構造をもつ代数系(特殊な亜群)などがある.
このエッシャー作品は,色の区別をしないとして幾何空間的に見れば,1つのトカゲのモチーフでできている.トカゲの左手の集まっている点には6回回転軸;
色を区別する超幾何空間なら3色の巡回置換の3回軸と色を保存する2回回転軸が共存する(これを$$6^{(3)}$$と表示).格子は単純な3角格子である.したがって,色の見分けができなければ古典群P6,色の見分けができれば$$P6^{(3)}$$の3色群である.空間群$$G$$には正規部分群として並進群Hが含まれる.$$H$$に関するラグランジュ展開の各剰余類を図解する.並進群$$H$$を法として同値とは,格子点に散らばっているトカゲを代表元1つにまとめることである.こうして,代表元系は,$$\{1,6,6^{2},\dots,6^{5}\}=G^*$$に同型な群をなす.
2次元の格子を,対称性で分類すると5種類(2次元ブラベー格子).2次元には,互いに独立な並進ベクトル2つがとれる.この2つの並進ベクトルの組を対称性で分類すると5種類になる.格子点間の垂直2等分線で囲まれる図形を「ディリクレ胞」というが,「ディリクレ胞」の形で分類したという見方もできる.
空間群には,正規部分群として並進群(格子)が含まれているので,並進群を結晶点群で拡大して空間群が得られる.組み合わされる点群は格子と両立する対称性のものである.一例として,直方(長方形)単純格子の格子点に,点群$$2mm$$の有限図形を配置して,空間群$$P2mm$$が得られる.
$$P2mm$$は共形群である.点群$$2mm$$の鏡映操作$$m$$を,映進操作$$g$$で置き換えることを考える.映進操作$$g$$とは,鏡映と鏡映面に沿った周期$$T/2$$の並進を組み合わせた操作のことである.したがって,映進を2回繰り返すと,$$g^{2}=T$$となり,格子分だけの移動になる.結晶格子は無限に繰り返すので,並進周期だけ移動した点はすべて同値である.そこで,映進操作,$$g^{2}=1(modT)$$は,周期的空間の対称操作となる.共型群$$P2mm$$から非共型群$$P2mg,P2gg$$が導ける.映進操作gは,非対称要素(モチーフ)を隣の胞に移動させてしまうが,格子を法と同値とすれば,単位胞内に(還元)引き戻せる.群$$G$$はその部分群$$H$$に関して剰余類の直和に展開(ラグランジュ展開)できる.特に,$$H$$が正規部分群である場合が重要で,剰余類は$$H$$を法として群(商群)をなす.
空間群の拡大では,正規部分群は非常に重要な役割を演ずる.$$H$$が$$G$$の正規部分群であるとき,$$H$$に関する剰余類は,$$H$$を法として商群$$G/H$$をなす.
逆に,$$\{a_{1}, a_{2}, \dots, a_{r }\}=G^{*}$$とし,群$$H$$を群$$G^*$$で拡大して群$$G$$を得る.
正規部分群$$H$$を群$$G^*$$で拡大して$$G$$が得られるのだが,$$G^*$$も正規部分群である場合は直積;$$G^*$$が非正規の部分群である場合には半直積;$$G^*$$が$$H$$を法として群となる(モジュラー群)の場合には条件積;で表現する.
19世紀末の3次元結晶空間群230種の数え上げは,20世紀結晶構造解析の基礎となる.古典群に関してはここで一段落とする.