[定義]部分群subgroup:
$$H$$が群$$G$$の部分群であるとは,次の条件1°,2°を満たすものである.
$$1 ^\circ $$ $$G \supset H$$
$$2 ^\circ $$ 群$$G$$の2項演算$$ \circ $$で,$$H$$が群をなす.
■$$H$$が群をなす条件は,次のどちらかと同値である:
$$2 ^\circ -1$$: $$a, b \in H$$$$ \to $$$$a \circ b \in H$$かつ$$b^{-1} \in H$$($$G$$が有限群ならば後者は不要)
$$2 ^\circ -2$$: $$a, b \in H$$$$ \to $$$$a \circ b^{-1} \in H$$
[演習]条件$$2 ^\circ -1$$と$$2 ^\circ -2$$は同値であることを証明せよ.
■$$2 ^\circ -2$$$$ \to $$$$2 ^\circ -1$$の証明
$$a, b \in H$$の条件は,$$b=a$$を選ぶと,$$a \circ a^{-1}=e \in H$$が成立つ.単位元が存在.
次に,$$e, b \in H$$から出発すると,$$e \circ b^{-1}=b^{-1} \in H$$が導かれる.$$b$$の逆元の存在.
最後に,$$a, b^{-1} \in H$$から出発すると,$$a \circ b \in H$$.
■$$2 ^\circ -1$$$$ \to $$$$2 ^\circ -2$$の証明
$$a, b \in H$$の条件から,$$b^{-1} \in H$$が成立つので,
次に,$$a, b^{-1} \in H$$から出発すると,$$a ^\circ b^{-1} \in H$$.
-----
[定義]商群
商群に関する定理
----------------------------------------
準同型写像とは
---------------------------------------------- \\
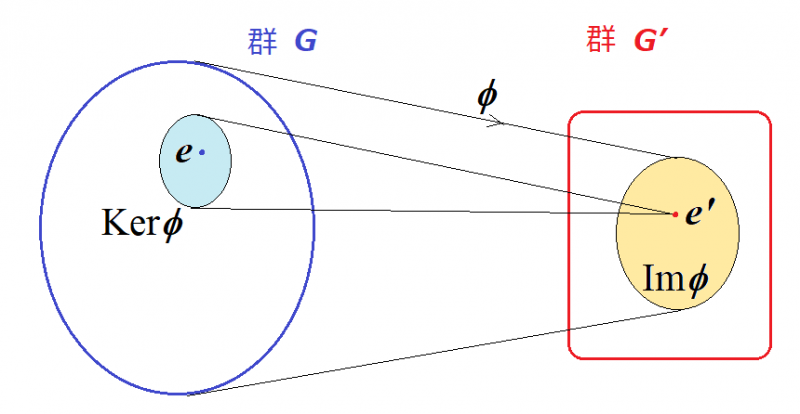
写像$$\phi $$は,群$$\left( G, \circ , e, x^{-1} \right) $$から群$$\left( G', \bullet , e', x'^{-1} \right) $$の中への準同型写像とします.
[準同型定理]
(1) $$G$$の像$$\textrm{Im}\phi $$は,$$G'$$の部分群になる.
(2) $$\phi ^{-1}(e') \equiv \textrm{Ker}\phi $$は,$$G$$の正規部分群になる.これを写像$$\phi $$の核kernelとよぶ.
(3) $$G$$の各元$$x$$の$$\textrm{Ker}\phi $$を法とする剰余類を$$\bar{x}$$とすると,剰余類$$\bar{x}$$ $$\to $$$$\phi (x)$$の写像は,
商群$$G/\textrm{Ker}\phi $$から群$$G'$$中の$$\textrm{Im}\phi $$への同型写像になる.
(証明)
(1) $$^{ \forall }a', ^{ \forall }b' \in \textrm{Im}\phi $$ $$\to$$ $$(a')^{-1}b' \in \textrm{Im}\phi $$を証明する.
$$^{ \exists }a, ^{ \exists }b \in G:a'=\phi (a), b'=\phi (b)$$
$$(a')^{-1}b'=\phi (a)^{-1}\phi (b)=\phi (a^{-1}b)$$
しかるに,$$a^{-1}b \in G$$であるから,$$(a')^{-1}b' \in \textrm{Im}\phi $$
(2) $$^{ \forall }u, ^{ \forall }v \in \textrm{Ker}\phi $$ $$\to$$ $$\phi (u)=\phi (v)=e'$$
$$\phi (u^{-1}v)=\phi (u)^{-1}\phi (v)=e'$$, ゆえに,$$u^{-1}v \in \textrm{Ker}\phi $$
よって,$$\textrm{Ker}\phi $$は$$G$$の部分群である.
$$^{ \forall }a \in G$$に対して,$$\phi \left( aua^{-1} \right) =\phi (a)\phi (u)\phi (a)^{-1}=e'$$
ゆえに,$$aua^{-1} \in \textrm{Ker}\phi $$
よって,$$\textrm{Ker}\phi $$は$$G$$の正規部分群である.
(3) $$^{ \forall }x_{1} \in \bar{x}$$に対して,$$^{ \exists }u \in \textrm{Ker}\phi $$があり,$$x_{1}=xu$$
$$\phi (x_{1})=\phi (x)\phi (u)=\phi (x)e'=\phi (x)$$
一つの剰余類に属する$$G$$の元の写像の行先は同一
$$^{ \forall }\bar{x}, ^{ \forall }\bar{y} \in G/\textrm{Ker}\phi $$(群)
$$\mit\Phi (\bar{x})\mit\Phi (\bar{y})=\mit\Phi (\bar{xy})=\phi (xy)=\phi (x)\phi (y)$$
$$\mit\Phi $$ は,$$G/\textrm{Ker}\phi$$ $$ \to $$$$\textrm{Im}\phi $$の準同型写像であることがわかったので,
これが,同型写像であることを証明するには.単射であること:
$$\mit\Phi (\bar{x})=\mit\Phi (\bar{y})$$ $$\to$$ $$\bar{x}=\bar{y}$$であることをいう.
$$\phi (x^{-1}y)=\phi (x)^{-1}\phi (y)=e'$$ ($$ \because \phi (x)=\phi (y)$$)
ゆえに,$$x^{-1}y \in \textrm{Ker}\phi $$,つまり,$$y=x \cdot \textrm{Ker}\phi $$ , $$\bar{y}=\bar{x}$$
[同型定理]
群$$G$$において,$$H$$を部分群とし,$$N$$を正規部分群とする.
このとき,
(1) $$HN(=NH)$$は$$G$$の部分群をなす.
(2) $$N$$は$$HN$$の正規部分群になり,
$$H \cap N \equiv D$$は$$H$$の正規部分群となる.
(3) $$HN$$中の$$N$$に関する剰余類は,$$hN$$の形に書かれる.
そして,これを$$H$$中の$$D$$に関する剰余類$$hD$$に写すとき,
商群$$HN/N$$から,商群$$H/D$$の上への同型が得られる:
$$HN/N \cong H/D$$
(証明)
( 1) $$(HN)^{-1}(HN)=N^{-1}H^{-1}HN=NHN=HNN=HN$$,$$HN \subset G$$は群.
$$N, H$$はそれぞれ群であるので$$N^{-1}=N, H^{-1}H=H$$,および,$$N \vartriangleleft G$$を用いた.
( 2) $$HN \vartriangleright N$$は自明.2つの部分群の共通集合は群をなすので$$D$$は群.
$$hDh^{-1} \subset hHh^{-1}=H$$,かつ,$$hDh^{-1} \subset hNh^{-1}=N$$
ゆえに,$$hDh^{-1} \subset D$$,$$H \vartriangleright D$$である.
( 3)剰余類の型$$hN$$は自明.
$$h_{1}N=h_{2}N \Longleftrightarrow h_{1}^{-1}h_{2}N=N \Longleftrightarrow \left. \begin{array}{@{\,} cc @{\, } }
& h_{1}^{-1}h_{2} \in N \\[0mm]
& h_{1}^{-1}h_{2} \in H
\end{array} \right\} \Longleftrightarrow h_{1}^{-1}h_{2} \in D \Longleftrightarrow h_{1}D=h_{2}D$$
同型写像: $$h_{i}N \longrightarrow h_{i}D$$