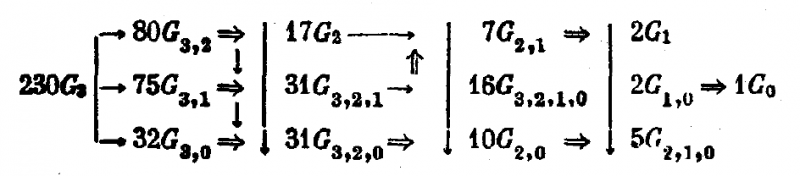3次元空間の対称性への移行準備のめに,これまでに研究されたすべてのタイプの群を統一的なスキームに統合しましょう.記号$$G_{r,s, \cdots ,t}$$は,$$r$$次元の幾何学空間の(等長)対称群であり,かつ,この群が,$$s, \ldots ,t\left( r>s> \cdots >t \right) $$次元の(周期的,または,非周期的)部分空間を,それぞれの中に変換するとします.この表記法で,片面ロゼット(第2章)の点群は,記号$$G_{3,2,0}$$(または,$$G_{3,1,0}$$)となります.なぜならば,この変換は,特異平面(2次元空間)と,それに垂直な(1次元空間)を,それぞれの中に変換し,同時に,特異点(0次元空間)を不変に保つからです.
有限(あるいは,無限)図形の点群$$G_{3,0}$$(第3章)は,3次元空間を自分自身の中に変換する一方,特異点だけを不変に保ちます.
群$$G_{3,0}$$から,3次元図形の異なる断面を考慮するか,棒の空間群$$G_{3,1}$$(第6章)の部分群を使って,群$$G_{3,2,0}$$に到着しました.両面平面による棒の(縦)断面は,両面帯群$$G_{3,2,1}$$(第5章)の対称性を決定します;後者からは,3次元空間を片面平面に投影して,片面帯$$G_{2,1}$$(第4章)の対称群へ進みます.
同様に,層群$$G_{3,2}$$から,網目パターンの空間群$$G_{2}$$(第7章)に移行します.
これらの群と,タイル($$G_{3,2,1,0}$$と$$G_{2,1,0}$$),片面ロゼット($$G_{2,0}$$),直線($$G_{1}$$),線分($$G_{1,0}$$),点($$G_{0}$$)対称群は,以下のスキームによって,互いに,かつ,3次元空間の対称群$$G_{3}$$(第9章)と関係づけられます:
図中,一重矢印は部分群への移行;二重矢印は断面,または,射影を示します.記号の前の数字は,離散的な結晶群の数.