繰り返し模様$$p3$$★

壁紙模様の対称性の第13番目の類は，対称性3の図形を，60°で交差する２つの等価な並進軸$$(a/a)$$で並進して得られる．

国際記号で$$p3$$，ロシア式記号で$$(a/a):3$$です．今回から始まる残り５つの対称性の類（第13~17）は，正3角形のメッシュに属します．

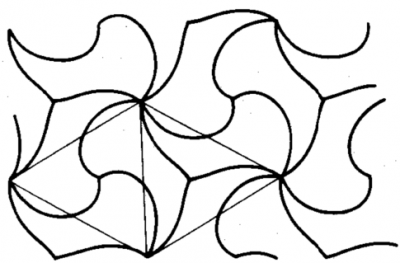
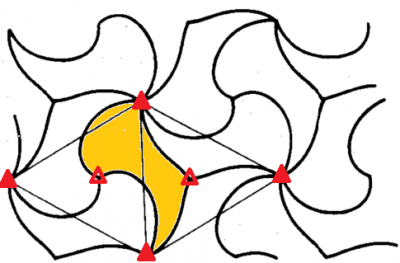
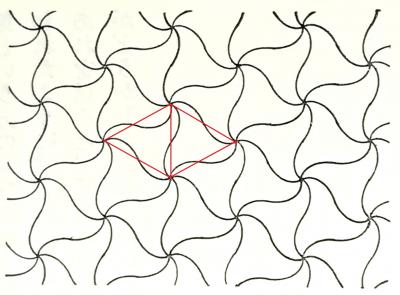
等価な図形が隙間なく平面を充填しているこの対称性のパターンを以下に示します．モチーフ（非対称要素）は，正3角形メッシュ座標を作っている頂点に集まる曲線で囲まれた形です．

非対称要素（モチーフ）３つで，単位胞の面積に等しくなります．鏡映対称はありません．

以下の例は，アルハンブラの有名なモザイクです．これは対称性$$p3$$の例です．ただし，色の区別はしていません．

（参考）以下の「千鳥」のパターンの対称性は$$p3$$ではありません．何故でしょうか？

（解答）上図の「ちどり」のパターンは，単位胞の菱形の頂点に6回軸がありますので，$$p3$$ではありません．このパターンは，後ででてくる$$p6$$の対称性です．単位胞の中を，2つの千鳥図形で埋まますが，この千鳥の形は，等価なモチーフにさらに3分割できますから，非対称要素は，千鳥を3分割したものになります．