同価点系
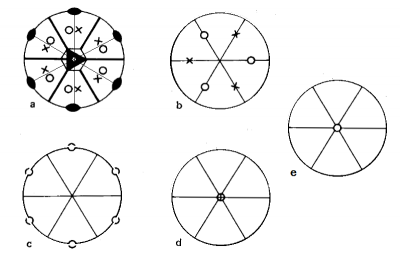
例として対称類$$\tilde{6} \cdot m$$を考察しよう.下図は対称類$$\tilde{6} \cdot m$$のステレオ投影図です.図aに記載されている対称要素は主軸$$\tilde{6} $$($$6$$回回映軸),鏡映面3枚$$m$$(太い線分),紙面内にある$$2$$回軸3本(基円上に両端が現れている),対称心$$\bar{1}$$があります.ステレオ投影は地図作りでも用いられますが,地球の表面の点を平面(基円内)に投影する方法でした.地球を北極側から見ていると想像しましょう.ステレオ投影の〇印は,北半球の表面にある点,×印は南半球にある点の投影像です.
球面上の1点に対称類(点群)の対称操作を作用させ生じる点の全体(同価点系,あるいは正則点系)を考察します.元の点を球面上で動かすと,他のすべての点も動きます.生じる同価点系の点の数は,元の点が対称要素の1つに当たるまで変わりません.
図aは,一般点に対称操作を作用させて生じた同価点のステレオ投影図です.全部で12個(=対称操作の数=群の位数)の同価点が生じています.
図bは,特殊位置(鏡映面上にある場合)に元の点がある場合で,ステレオ投影で生じる同価点の数は6個と半減しました.
図cは,特殊位置($$2$$回軸上ある場合)に元の点がある場合で,ステレオ投影で生じる同価点の数は6個です.やはり半減しました.
図dは,元の点が3回軸と3つの対称面上にある場合で,同価点の総数は6分の1になります.
図eのように,元の点が,すべての対称要素が交差する特異点にある場合ならば,対称操作により生じる点はすべて重なってしまうので,ステレオ投影で生じる点も1点です.この点の多重度は12.
1つの点に重なる同価点の数を,その点の多重度と呼びます.
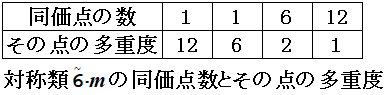
同価点の系(正則点系)で,点の多重度とその点の同価点数の積は一定で,群の位数になります.(対称類$$\tilde{6} \cdot m$$の位数は12)
図a,b,c,d,eの正則点系を構築する際に,対称類は同じままであるという仮定がありました.しかし,図b,cの点系を比較すると,これらは異なる対称性を持っことがわかります:例えば,図bの系には3回軸があり,図cの系には6回軸があります.このように一見矛盾しているように見えるのは,まだ点自体の対称性を無視しているからです.点は〇で表現されていますが,実際には〇ではなく,図a,b,c,d,eの5つの系で,点の対称性は全く異なっています.
図aでは,点(一般点と呼ぶ)はどの対称要素にも乗っておらず,その多重度は1で,完全に非対称である.図bの系では,元の点は対称面m上に位置し,点の対称性は鏡映対称mです;図cの系の点は,2回対称を持ちます.図dでは,点の対称性は3・mを持ちます.
以上,対称類~6・mを例にして,適当に選んだ1点に対称操作を作用させて,同価点の系(正則点系)を作りました.これを,単純点系といいます.これに対して,複合点系というのは単純点系の組み合わせで作れます.
それぞれの種類の点は,独自の同価点系を形成し,異なる系に属する点は互いに同価ではありません.
複合系の記述には,点の多重度の相対比が重要です.例えば,多重度が2,6,12の3つの単純系からなる複合系があったとしましょう.この相対比は,1,3,6となる.この数は化学組成において重要な役割を果しています.すべての分子は,数学的近似において「点」と見做せる原子またはイオンよりなりますから,同価な原子(イオン)は1つの単純形をつくり,構成原子(イオン)の相対比はそれらの原子(イオン)が占める位置の対称性の制約となります.
注意が必要なのは,元の点の位置が固定されるのは,対称軸の交点,つまり球の中心にあるときのみということです.この場合にのみ,その対称類でただ1点の同価点系を得ることができます.
それ以外の場合は,元の点の位置は,その形で点の数を変えることなく,無限に存在します.言い換えれば,2点,6点,12点の正則系が無数存在します.
図72に示した正則点の系を構築する際には,すべての点の系において対称類が同じままであるという仮定から始めた.図72b,cの系を比較すると,これらは異なる対称性を持っていることがわかる:例えば,図72bの系には3回軸があり,図72cの系には6回軸があります.このように一見矛盾しているように見えるのは,まだ点自体の対称性を無視しているからであり,これらはいずれも誤って円として表現されている.実際には,4つの系では,点の対称性は全く異なっています.図72aでは,点はどの対称要素にも乗っておらず,その多重度は1に等しいので,完全に非対称である.図72bの系の点は二回対称で,対称面上に位置し,それぞれ対称性mを持つ;図72cの系の点は対称性2を持つというように異なっている.点の対称性については,後で詳しく議論する.
以上,図72の例を用いて,(適当に選んだ1つの点を繰り返すことで生じる)単純な点の系がどのように作られるかを示した.単純なシステムから,複雑な複合システムに移行することは難しくありません.後者の場合,球体上または球体内にいくつかのタイプの点があります.
それぞれの種類の点は,同価な点の独自の系を形成し,異なる系に属する点は互いに等しくない.
複合系の記述には,点の相対的な数が重要な役割を果たすが,その数がどのようにして得られるかを見てみよう.例えば,2点,6点,12点の3つの単純系からなる複合系があったとする.この相対数は,これらを2の共通因子で還元して,1,3,6となる.後述するように,この数は化学において重要な役割を果たしている.というのも,すべての分子は,数学的近似において「点」とされる同価な原子またはイオンの複雑な対称系とみなすことができるからである.
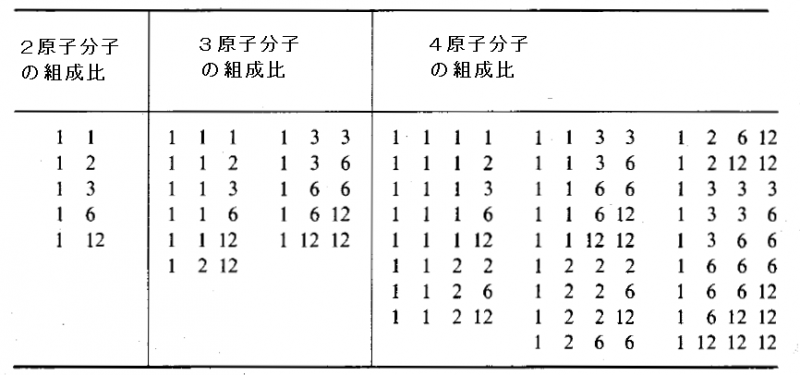
この計算により,例えば,対象とする対称性類について,2種類,3種類,4種類の非等価な点を含む複合系の相対数を表3に示す.
(Picture)
物質は分子で構成されており,分子は原子,イオン,ラジカルなどで構成されていることはよく知られている.科学的な化学が始まった当初から,同一の性質を持つ化学分子の部分は同一の(対称的な)位置を占めると考えるのが通例であった.この考え方は,少数の化学元素を扱うことが多い有機化学では特に有効であり,次のような場合には同一元素の原子を識別する必要がある.
例えば,CH3COOHという式で表される酢酸の分子では,炭素記号Cが2回現れるが,この2つの炭素原子の違いを明示するためである.
酢酸の性質を調べると,1つの分子には4つの水素原子Hが含まれており,そのうち3つの水素原子は化学的性質が等しいが,4つ目の水素原子は異なる.
酢酸の式では,記号Hが2回使われているが,そのうち1回のHには添字3がついている.
ラウエがX線回折を発見し,結晶や分子の構造解析法が開発された後,分子や結晶格子の構造単位が対称的に配置されていることが実験的に確認され,構造化学や結晶化学への対称性理論の応用は広大な分野となった.
原子(ラジカル)を点(あるいは図形)で仮に表すと,分子は点(図形)の規則的な(単純,あるいは複合的な)系である.分子の対称類と,同じ性質を持つ原子の種類の数がわかっていれば,対称類と矛盾しない化学式を事前に決めることができる.
例えば,ある化学分子が,性質の異なる2種類の原子AとBから構成されており,その対称性が$$\tilde{6} \cdot m$$であることがわかったとする(図72).この対称性類を満たす化学式はすべて候補となる.
言い換えれば,2元系化合物$$A_{n}B_{m}$$の式に含まれる係数nとmをすべて計算しなければならない.同一の原子が分子内の単純系の点を占めると仮定すると,係数nとmは,複合系を形成する単純系の点の相対比となる.相対比の表(表3)を見ると,この場合のすべての公式を簡単に書き出すことができる.
$$A_{1}B_{1} ; A_{1}B_{2} ; A_{1}B_{3} ; A_{1}B_{6} ; A_{1}B_{12}$$
これらの式は,化学的に等価な原子が構造的に等価でない場合,すなわち,A型とB型の原子がそれぞれ構造的に区別される場合に;$$A_{n1}, A_{n2}, \cdots , A_{ni} , B_{m1}, B_{m2} , \cdots , B_{mj}$$に分かれていると,より複雑な状況になる.この場合の2元化合物$$A_{n1}A_{n2} \cdots A_{ni} B_{m1}B_{m2} \cdots B_{mj}$$は,再分割された原子のそれぞれが単純系を占めている.