今回は,平面群の第4類の説明です.この類は,直交する2つの映進面がありますので複雑です.
映進面が1つのパターン$$pg$$の例を参照ください.
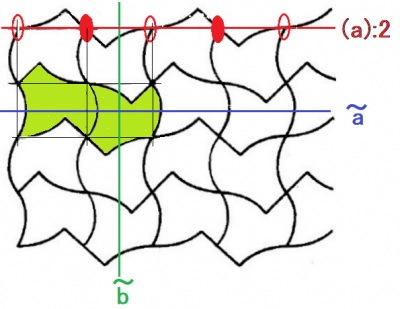
以下のペルシャのパターンが,$$pgg2$$の繰り返し模様の例です.
国際記号で$$pgg2$$,ロシア式記号で$$(b:a):\tilde{b}:\tilde{a}$$と書かれるものです.
[構成方法1]
① 2回対称軸が$$a$$軸方向に周期的に配列した1次元構造(図の1番上の行にあります);
この対称性は$$(a):2$$
② この1次元構造を,$$b$$軸($$a$$軸に垂直)に沿って映進$$\tilde{b}$$すると,2次元のパターンが得られます. 対称性$$( b:a) :\tilde{b}:\tilde{a}$$
(注) 1次元構造$$( b) :2$$を映進$$\tilde{a}$$で繰り返し広げても同じ構造が得られます.
[構成方法2]
互いに直交する2つの映進面$$\tilde{a}$$,$$\tilde{b}$$が作用すると,
このパターン$$( b:a) :\tilde{b}:\tilde{a}$$が得られます.
上記の2つの構成方法を等しいと置くと,$$\tilde{b}:\tilde{a}=2 \odot \tilde{a}$$となり
これは,点群$$2m$$に同型な,拡張された点群であることがわかります.
(注)$$\odot $$
2つの直交する映進面$$\tilde{a}$$と$$\tilde{b}$$の組み合わせは,
交差する直線(不動線)がありますが,2回軸$$2$$と映進面$$\tilde{a}$$の組み合わせは,
互いに平行で交差しません.
記号$$ \odot $$は交差しない対称操作の組み合わせであるときに用いる記号です.
(注)拡張された点群
$$\tilde{b}:\tilde{a}$$の組み合わせも,$$2 \odot \tilde{a}$$の組み合わせも,それらの対称操作を繰り返すと
並進の成分が生まれます.そのため,格子分だけ移動したものは同値としないと点群になりません.このような拡張された点群は,格子を核として写像すると点群に帰着できます.この場合は群$$2m$$と同型になります.