技術的な応用●ブラッグの法則 ●干渉
10cm×10cm程度の薄い布(ナイロン,カプロン,絹)を2枚重ねて,繊維が小さな角度(5°-10°)で交差するようにする.これを2枚のガラス板の間に挟み透過光で全体を観察すると,モアレパターンと呼ばれる自然界で広く見られる現象(科学技術で頻繁に利用される)が観察できる(図151).モアレパターンの対称性乱れは,干渉を起こすネットの不完全性に起因するものである.もし,これらが完全に規則的なネットならば,不規則なモアレではなく規則的な二次パターンが現れる.この現象は,写真印刷などで,ガラス板の上に細かい黒格子が描かれたスクリーンを通して写真を撮影するハーフトーン印刷で見られる.
Fig.151
しかし,「スクリーン効果」は必ずしも作品の邪魔をするものではなく,布地や壁紙などで優れたパターンを作るために使われることもある.
■2 つの無限平面パターンを重ね合わせたときに,どのようにして二次的なパターンが発生するのかを理解するために,最も単純な例として2 つの同一な平行縞を重ね合わせた場合の例を見よう.図152に示すように,2つの1次元縞の相互作用(干渉)の結果,一次の縞(元の縞)の繰り返し周期よりも大きな繰り返し周期の二次的な幅広の縞が生成される.実際には,これらの二次的な幅広縞は,一次の縞によって形成されたジグザグに過ぎない.一次の縞の間隔を,目で解像できない程度(0.1mm以下)まで小さくすることで,二次的な縞だけが見える画像が得られるが,これは一次の縞の一つを拡大したものになる.
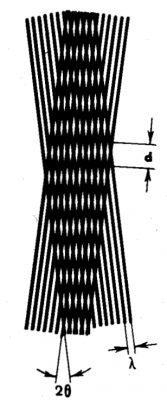
一次縞周期(一本の縞の幅+縞間の間隔)を$$λ$$,二次縞周期 を$$d$$,一次縞系が交差する角度$$2θ$$ とすると,簡単な計算で,$$λ=2dsinθ$$ が得られる.
すなわち,一次縞周期は,二次縞周期の2倍に一次縞間の交差角度の半分の$$sin$$を乗じた値に等しい.
Fig.152
結果として得られる式は,よく知られているブラッグの法則と全く同じになる.ブラッグの法則中の量λはX線の波長であり,$$d$$はX線を反射する結晶の原子網面の間隔,$$θ$$は入射X線と反射面の間の角度である.
このアナロジーで,結晶構造の幾何学のX線による研究を,モアレ現象に還元することができる. [例えば,Bollmannの本(1970)を参照]
■今度は,平行縞の2つの系を2つの同一正方形の網にしよう.交差角2θが十分小さな角度なら,2次的に生じる像は,最初の網を単純に拡大した,少しぼやけた像になる(図153).
図153
一次の系の網目4角形の辺は,以下のように計算できます.
一次ネットと回転した一次ネットを重ねて生じる二次のネット網目の寸法に関しては,既に述べた1次元での関係がやはり成立します.
上記の2つのケースの図柄の重ね合わせで,角度$$±2θ$$の小さな角度で重ね合わせても,$$180°±2θ$$で重ね合わせても違いがなかったのは,図柄に2回回転対称性があるためである.
2回回転対称のない図形,例えば,3角形の系(図154)を重ね合わせるとすると,この二つの回転角度の効果にはかなりの差がでる.
小さな回転角$$2θ$$では,二次的な絵柄(図155)は楕円の系のようなものであるのに対し,回転角$$180±2θ$$では,二次的な絵柄(図156)は三角形で構成されて,一次的(元の)な絵柄の拡大と考えてもよい.
図154
図155
図156
図157
図158
詳細に検討してみると,角度$$2θ$$が十分に小さく,一次パターンが周期的に繰り返される小さな素図形をかなりの数持っている場合には,$$180°±2θ$$の角度で2つの同一のパターンを重ね合わせると,無限の対称平面パターンが拡大された形で得られることがわかる.
実際には,これらの条件を満たすことは非常に困難なことが多いので,この実験は最も単純な種類の素図形でしか合理的な成功はしません(図157と158).