両面帯の対称性

■両面帯two-sided band

帯とは無限に続く周期図形で，１つの特異平面と，その平面内の１つの特異並進があります．
片面帯one-sided bandはその特殊なケースで，特異平面に極性があり，その表面は裏面と異なります
[１つの表面しかありません]．
一般の帯では特異面は非極性であり，表裏の面を互いに重ねる変換が許されています．
許される変換のリストにこのような変換が追加されると，1次元の帯飾りに適用される対称類の数は，
片面帯の７つの対称類に加えて，非極性面をもつ両面帯の24の対称類が追加されます．
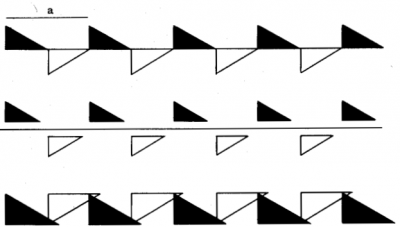
両面帯では，新しい対称要素；2回らせん軸が出現します．

■位数２のらせん軸
白と黒は3角形の表面と裏面を表します．

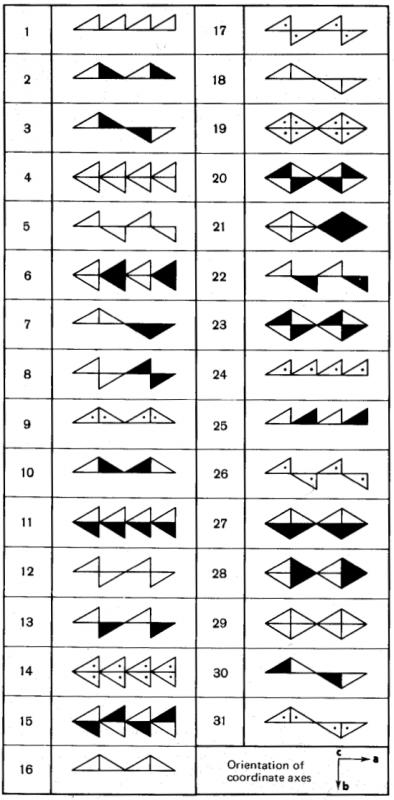
 ■両面帯の全部で31種類の対称類のパターンを，3角形モチーフの配列で表した一覧表を示します．
１，４，５，12，16，18，29の7種は，片面帯ですでに出現した対称類で，
残りの24種は，両面帯になって出現した対称類です．
（白面と黒面で表と裏を表しています．ドットのついた面は，表面と裏面が重なっている状態を表現しています）

帯のすべての対称類31種は，６つの対称要素６つの対称要素
$$a, 2, 2_{1}, m, \tilde{a}, \tilde{2}=\bar{1}$$　の独立な組み合わせで生成されます．
これら31個は，1次元の空間群と呼ばれます．

■両面帯に使われる以下のモチーフの対称性は？

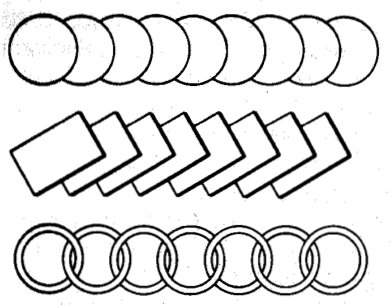
■紙から対称帯を切りとる
以下の3つの例a,b,cの縁飾りは，紙をどのように折って切ったのでしょうか？
折り目になった線は対称面になるはずですね．