繰り返し模様$$pmg2$$★

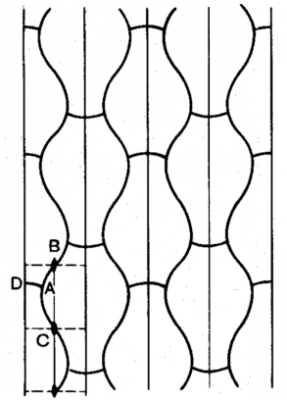
繰り返し模様の対称性の第５類は，
国際記号で$$pmg2$$，ロシア式記号で$$(b:a):m:\tilde{a}$$ 
（$$a$$の上に~を載せた記号$$\tilde{a}$$を,Texがつかえない場所では~$$a$$のように書くことにします）

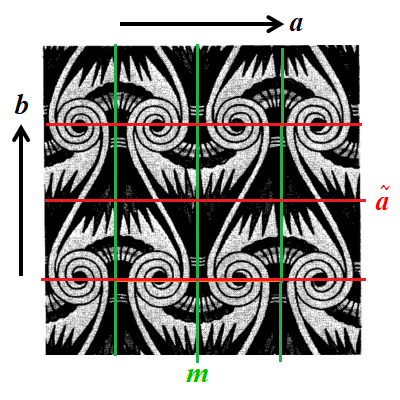
 垂直な帯$$(b)･m$$を，水平方向のa軸に沿った映進面$$\tilde{a}$$で繰り返すことで得られる．
対称性の記号は$$(b:a):\tilde{a}:m$$と記述できる．上図に示したのはこの対称性のパターンの例です．このパターンの中で，つながっている２つのコイル状の曲線に注目しよう．一つは，s字の形になり，他方は逆s字の形になっている．2回回転軸は紙面に垂直で，S字曲線の中心とコイルの中心を通っています．尖った葉を束ねて尖った葉の先端が上を向いたり下を向いたりしています．
帯の対称性$$(b)･m$$は，$$(b):2$$　とも書けるし，映進面$$\tilde{a}$$は2回軸を面内に含むので，この2次元のパターンの対称性は，$$(b:a):m:\tilde{a}=(b:a):2･\tilde{a}$$　と記述できます．

束ねた葉の尖った先端を上に向けたり下に向けたりしているパターンは，蓮の花の円錐形のデザインでエジプトの伝統模様に見られます．

以下の模様も同じ対称性です．

（注）拡張された点群$$2･\tilde{a}$$は，格子分並進したものは同値と見なすことにすれば，点群$$2･m$$に同型です．映進面$$\tilde{a}$$の中に2回軸が含まれるので，記号$$ ⊙ $$を用いる必要はありません．